
© Ivana Martic, MATH+
Rules and infos regarding the bonus challenge
- There are no points for this challenge
- You can submit answers until the 30. december 11:59:59 pm (CET)
- Among all correct answers, we will raffle off a book about geometry.
Author: Felix Günther
Project: EF 2-1
Challenge
Santa Claus wants to beautify his office and add a new glass roof to it. The hole in the ceiling, where the glass roof is to be placed, has the shape of a regular hexagon. Now Santa has six triangular glass plates in mind, which should be artfully assembled for the roof. It is important to him that the reflections of the roof in sunlight are uniformly beautiful and have no breaks. Therefore, the outer edges of the glass plates do not necessarily have to be parallel to the edges of the hexagonal hole; the plates can also be set at an angle. Due to the cold polar nights, Santa’s ceiling is very thick.
To implement his plan, he hires the architecture firm MA&TH+, founded by the architecture elf Theresa and the mathematician elf Maryna. Maryna translates Santa’s requirements into mathematics: “So you want to arrange six triangular surfaces in the shape of a star: they have exactly one point in the middle in common, and at the edges, they fit together accordingly. For simplicity, let’s call this figure a cone, even though it’s not particularly round. The reflections of the cone in sunlight are determined solely by the position and arrangement of its side surfaces. Similarly, we can consider the normal vector for each of the six triangles: this is a vector (displacement arrow) of length 1 that is perpendicular to the respective surface and is outward pointing, i.e. pointing towards the sky. If we connect neighboring normal vectors on the surface of the sphere with radius 1, a spherical polygon is created, which we also call the normal image. The reflections of the cone in sunlight are uniformly beautiful if the normal image does not intersect itself.”
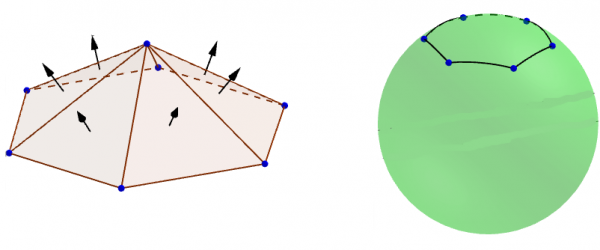
Figure 1: A pyramid as a glass roof and its normal image
Theresa suggests a regular pyramid as shown in Figure 1 as a glass roof. This construction has proven itself and precisely meets Santa’s requirements – after all, the normal image is a regular spherical hexagon and, in particular, free of self-intersections. However, Santa finds this too boring. He envisions a more interesting shape, even though he cannot describe it very well. Therefore, he draws various spherical polygons that he would find exciting as normal images (see Figure 2). At first glance, however, Maryna and Theresa cannot say which of these correspond to a suitable cone.

Figure 2: The spherical polygons of Santa Claus
Maryna and Theresa retreat to their office for consultation. They discuss the matter with their elf colleagues Aylin and Niveditha. Aylin remembers a recently proven theorem that could be helpful for Santa’s problem. This theorem states that the oriented area F of the normal image is equal to 2\pi minus the sum of the interior angles of the triangles adjacent at the common vertex, where all angles are measured in radians. The orientation of the area is to be understood as follows: if we traverse the side surfaces of the cone counterclockwise, the area of its normal image is positive when we traverse the spherical polygon counterclockwise and negative when we traverse it clockwise. For example, the normal image of the regular pyramid has a positive area.
Now Niveditha speaks up: “By the way, the (non oriented) area of a spherical polygon that does not intersect itself can be easily calculated from the angles of the polygon! For our polygon, we just have to add up the interior angles and subtract 4\pi from the result.
With this assistance, Maryna and Theresa enthusiastically start figuring out which spherical polygons drawn by Santa can be realized as normal images of a possible glass roof. After a while of pondering, they find out that they can relate the angles at the common vertex of the cone to the interior angles of the spherical polygon. Intrigued by their discovery, they go to their elf colleagues and explain what they have found: “If we number the side surfaces of the cone counterclockwise with f_1 to f_6, name the angles at the common vertex of the cone with \alpha_1 to \alpha_6 according to the names of the side surfaces, and also denote the interior angles of the spherical polygon with \beta_1 to \beta_6, then we can distinguish two cases: Either the area of the polygon is positively oriented or negatively oriented. In the first case, we can consider a triangle of the cone, e.g., f_3. The neighboring triangles f_2 and f_4 must then either be on the same side of f_3 or on different sides. If they are on the same side, then we have found that \beta_3 = \pi - \alpha_3 holds, and that \beta_3 < \pi, but if they are on different sides, then \beta_3 = 2\pi - \alpha_3 and \beta_3 is an obtuse angle. Of course, this also applies to all other triangles f_1, f_2, etc. If, on the other hand, the area of the spherical polygon is negatively oriented and the neighboring triangles of, for example, f_3 are on the same side, then \beta_3 = \pi + \alpha_3 holds, and \beta_3 is an obtuse angle, and if they are on different sides, then \beta_3 = \alpha_3 and \beta_3 < \pi.”
\begin{array}{|c|c|c|}\hline& F\, \mathrm{positive} & F\, \mathrm{negative}\\\hline \text{same side} & \beta = \pi - \alpha, \beta<\pi & \beta = \pi + \alpha, \beta > \pi \\\hline \text{different sides} & \beta = 2\pi - \alpha, \beta > \pi & \beta = \alpha, \beta < \pi\\\hline\end{array}
Aylin and Niveditha examine Maryna and Theresa’s calculations and agree with them: “Great! That means you just have to figure out which combinations of triangles with neighboring triangles on the same or different sides are possible.”
Which spherical polygons drawn by Santa can be realized as normal images of a possible glass roof? Santa’s ceiling is so thick that it does not impose any significant restrictions on the glass roof. (For your construction, you can assume that the ceiling is infinitely thick.)
Possible Answers
- Only the first.
- Only the second.
- Only the third.
- Only the fourth.
- Only the fifth.
- Only the first, second, and third.
- Only the first, second, and fifth.
- Only the second and third.
- All except the first.
- All five.
In the project EF 2-1 “Smooth Discrete Surfaces”, we dealt with surfaces composed of flat polygons that behave like smooth surfaces. Our initial assumption was that the normal image around each vertex should be free of self-intersections. This discretization is motivated by the classical theory of smooth surfaces, where the normal image is also locally free of self-intersections, provided that the curvature at a vertex is not 0. Based on further analogies to smooth surfaces, we developed a theory of “smooth discrete surfaces.” This theory is relevant for applications in architecture. For instance, architects want to design curved glass facades, but due to cost reasons, they rely on realizations using glass plates. It is quite expensive and complex to bend glass on a large scale. Therefore, they are interested in polyhedral surfaces that share many properties with smooth surfaces – among other things, the reflections in sunlight should be uniform. An algorithm based on our theory improves designs of glass surfaces in terms of their reflections.
The theorem mentioned in the task about the oriented area of the normal image also played a crucial role in our work. However, there was no general proof of this statement before – only a proof for special cases, such as the convex case from Figure 1, was known. We were eventually able to find an elementary proof, which was published in the American Mathematical Monthly: https://www.tandfonline.com/doi/full/10.1080/00029890.2023.2263299