Bonus: Wer im Glashaus sitzt…

© Ivana Martic, MATH+

Regeln und Infos zur Bonusaufgabe

• Diese Aufgabe bringt keine Punkte.
• Die Abgabe einer Antwort ist bis zum 30.12. 23:59:59 (MEZ) möglich.
• unter allen richtigen Antworten verlosen wir das Buch “Perlen der Mathematik”

Autor: Felix Günther

Projekt: EF 2-1

Aufgabe

Der Weihnachtsmann möchte seine Schreibstube verschönern und sie mit einem neuen Glasdach versehen. Das Loch in der Decke, auf welches das Glasdach gesetzt werden soll, hat die Form eines regelmäßigen Sechsecks. Dem Weihnachtsmann schweben nun sechs dreieckige Glasplatten vor, die für das Dach kunstvoll zusammengesetzt werden sollen. Dabei ist ihm wichtig, dass das Glasdach sich von außen gut in die Umgebung einpasst. Für den Weihnachtsmann heißt das, dass die Reflexionen des Dachs im Sonnenlicht schön gleichmäßig und keine Brüche aufweisen sollen. Dafür müssen die äußeren Kanten der Glasplatten nicht parallel zu den Kanten des sechseckigen Loches sein, die Platten dürfen auch schräg eingesetzt werden. Aufgrund der kalten Polarnächte ist die Decke des Weihnachtsmannes nämlich sehr dick.

Für die Umsetzung seines Plans engagiert er das vom Architekturwichtel Theresa und vom Mathematikwichtel Maryna gegründete Architekturbüro MA&TH+. Maryna übersetzt die Anforderungen des Weihnachtsmannes ins Mathematische: “Du möchtest also sechs dreieckige Flächen in der Form eines Sterns anordnen: Sie haben genau einen Punkt in der Mitte gemeinsam und an den Kanten passen sie entsprechend aneinander. Diese Figur nennen wir der Einfachheit halber Kegel, auch wenn er nicht sonderlich rund ist. Die Reflexionen des Kegels im Sonnenlicht werden allein durch die Position und Anordnung ihrer Seitenflächen bestimmt. Genauso können wir für jedes der sechs Dreiecke seinen Normalenvektor betrachten: Dies ist ein Vektor (Verschiebungspfeil) der Länge 1, der senkrecht auf der jeweiligen Fläche steht und nach außen Richtung Himmel zeigt. Wenn wir benachbarte Normalenvektoren auf der Oberfläche der Kugel mit Radius 1 verbinden, so entsteht ein sphärisches Polygon, welches wir auch Normalenbild nennen. Die Reflexionen des Kegels im Sonnenlicht sind genau dann gleichmäßig, wenn sich das Normalenbild nicht selbst überschneidet.”

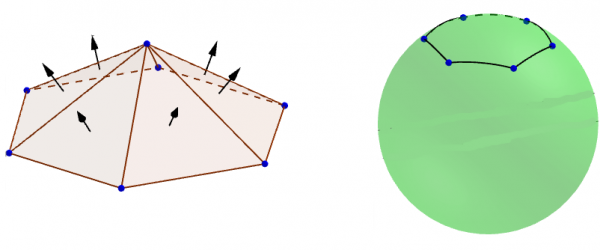
Abbildung 1: Eine Pyramide als Glasdach und ihr Normalenbild

Theresa schlägt eine regelmäßige Pyramide wie in Abbildung 1 als Glasdach vor. Diese Konstruktion habe sich bewährt und erfordert genau die Anforderungen des Weihnachtsmannes – immerhin ist das Normalenbild ein regelmäßiges sphärisches Sechseck und insbesondere frei von Selbstschnitten.

Dem Weihnachtsmann ist dies allerdings zu langweilig. Ihm schwebt eine interessantere Form vor, auch wenn er sie nicht so gut beschreiben kann. Daher zeichnet er verschiedene sphärische Polygone, die er als Normalenbilder spannend fände (siehe Abbildung 2). Auf Anhieb können Maryna und Theresa jedoch nicht sagen, welche von denen zu einem geeigneten Kegel gehören.

Abbildung 2: Die sphärischen Polygone des Weihnachtsmannes

Maryna und Theresa ziehen sich zur Beratung in ihr Büro zurück. Sie besprechen sich mit ihren Wichtelkolleginnen Aylin und Niveditha. Aylin erinnert sich an einen kürzlich bewiesenen Satz, der für das Problem des Weihnachtsmannes hilfreich sein könnte. Dieser besagt, dass der orientierte Flächeninhalt F des Normalenbilds gleich 2\pi minus der Summe der an der gemeinsamen Ecke angrenzenden Innenwinkel der Dreiecke entspricht, wobei alle Winkel im Bogenmaß gemessen werden. Die Orientierung des Flächeninhalts ist dabei wie folgt zu verstehen: Gehen wir die Seitenflächen des Kegels gegen den Uhrzeigersinn entlang, so ist der Flächeninhalt seines Normalenbildes positiv, wenn wir das sphärische Polygon gegen den Uhrzeigersinn abschreiten, und negativ, wenn wir das sphärische Polygon im Uhrzeigersinn abschreiten. Zum Beispiel hat das Normalenbild der gleichmäßigen Pyramide einen positiven Flächeninhalt.

Nun meldet sich Niveditha zu Wort: “Der (nicht orientierte) Flächeninhalt eines sphärischen Polygons, welches sich nicht selbst schneidet, lässt sich übrigens ganz einfach über die Winkel des Polygons ausrechnen! Für unser Polygon müssen wir dafür nur die Innenwinkel addieren und vom Ergebnis 4\pi subtrahieren.”

Mit dieser Hilfestellung fangen Maryna und Theresa motiviert an, herauszufinden, welche sphärischen Polygone des Weihnachtsmanns sich als Normalenbilder eines möglichen Glasdachs realisieren lassen. Nach einer ganzen Weile des Überlegens, finden sie heraus, dass sie die Winkel an der gemeinsamen Ecke des Kegels in Beziehung mit den Innenwinkeln des sphärischen Polygons bringen können. Fasziniert von ihrer Entdeckung gehen sie zu ihren Wichtelkolleginnen und erklären ihnen, was sie herausgefunden haben: “Wenn wir die Seitenflächen des Kegels gegen den Uhrzeigersinn mit f_1 bis f_6 nummerieren, sowie die Winkel an der gemeinsamen Ecke des Kegels mit \alpha_1 bis \alpha_6 passend zu den Namen der Seitenflächen nennen und ebenso die Innenwinkel des sphärischen Polygons mit \beta_1 bis \beta_6 bezeichnen, dann können wir zwei Fälle unterscheiden: Entweder der Flächeninhalt des Polygons ist positiv orientiert oder negativ orientiert. Im ersten Fall können wir dann ein Dreieck des Kegels betrachten, z.B. f_3. Die Nachbardreiecke f_2 und f_4 müssen dann entweder auf der gleichen Seite von f_3 sein oder auf unterschiedlichen. Wenn sie auf der gleichen Seite liegen, dann haben wir herausgefunden, dass \beta_3 = \pi - \alpha_3 gilt und das \beta_3 < \pi, aber wenn sie auf unterschiedlichen Seiten liegen, dann gilt \beta_3 = 2\pi-\alpha_3 und \beta_3 ist ein überstumpfer Winkel. Natürlich gilt das auch für alle anderen Dreiecke f_1,f_2, etc. Wenn der Flächeninhalt des sphärischen Polygons dagegen negativ orientiert ist und die Nachbardreiecke von z.B. f_3 auf der gleichen Seite liegen, dann gilt \beta_3 = \pi + \alpha_3 und \beta_3 ist ein überstumpfer Winkel, und wenn sie auf unterschiedlichen Seiten liegen, dann gilt \beta_3 = \alpha_3 und \beta_3<\pi.”

\begin{array}{|c|c|c|}\hline& F\, \mathrm{positiv} & F\, \mathrm{negativ}\\\hline \text{gleiche Seite} & \beta = \pi - \alpha, \beta<\pi & \beta = \pi + \alpha, \beta > \pi \\\hline \text{unterschiedliche Seiten} & \beta = 2\pi - \alpha, \beta > \pi & \beta = \alpha, \beta < \pi\\\hline\end{array}

Aylin und Niveditha schauen sich die Berechnungen von Maryna und Theresa an und stimmen ihnen zu: “Super! Das heißt, ihr müsst jetzt nur noch herausfinden, welche Kombinationen von Dreiecken mit Nachbardreiecken auf der gleichen oder auf unterschiedlichen Seiten möglich sind.”

Welche sphärischen Polygone des Weihnachtsmannes lassen sich als Normalenbilder eines möglichen Glasdachs realisieren? Die Decke des Weihnachtsmannes ist dabei so dick, dass das Glasdach hierdurch keinen nennenswerten Einschränkungen unterliegt. (Ihr dürft für eure Konstruktion also annehmen, dass die Decke unendlich dick ist.)

Antwortmöglichkeiten

1. Nur das erste.
2. Nur das zweite.
3. Nur das dritte.
4. Nur das vierte.
5. Nur das fünfte.
6. Nur das erste, zweite und dritte.
7. Nur das erste, zweite und fünfte.
8. Nur das zweite und dritte.
9. Alle außer dem ersten.
10. Alle fünf.

Projektbezug

Im Projekt EF 2-1 “Smooth Discrete Surfaces” haben wir uns mit aus flachen Polygonen zusammengesetzten Flächen beschäftigt, die sich wie glatte Flächen verhalten. Unsere erste Annahme war, dass das Normalenbild um jede Ecke herum frei von Selbstüberschnitten sein soll. Diese Diskretisierung ist aus der klassischen Theorie von glatten Flächen motiviert, bei der das Normalenbild lokal ebenfalls frei von Selbstschnitten ist, sofern die Krümmung an einer Ecke nicht 0 ist. Mittels weiterer Analogien zu glatten Flächen haben wir eine Theorie “glatter diskreter Flächen” entworfen. Diese Theorie ist für Anwendungen in der Architektur relevant. So möchten Architektinnen geschwungene Glasfassaden konstruieren, aus Kostengründen sind sie aber auf Realisierungen mittels Glasplatten angewiesen. Es ist nämlich recht aufwendig und teuer, Glas im großen Maßstab zu verbiegen. Daher sind sie an polyedrischen Flächen interessiert, die viele Eigenschaften mit glatten Flächen gemeinsam haben – unter anderem sollen die Reflexionen im Sonnenlicht gleichmäßig sein. Ein auf unserer Theorie aufbauender Algorithmus verbessert Entwürfe von Glasflächen in Hinblick auf ihre Reflexionen.

Der in der Aufgabe erwähnte Satz über den orientierten Flächeninhalt des Normalenbildes spielte auch für unsere Arbeit eine wichtige Rolle. Allerdings existierte zuvor kein allgemeiner Beweis dieser Aussage – nur für Spezialfälle wie den konvexen Fall aus Abbildung 1 war ein Beweis bekannt. Wir konnten schließlich einen elementaren Beweis finden, welcher im American Mathematical Monthly publiziert wurde: https://www.tandfonline.com/doi/full/10.1080/00029890.2023.2263299