
© Friederike Hofmann, MATH+
Authors: Olaf Parczyk, Silas Rathke (FU Berlin)
Project: Learning Extremal Structures in Combinatorics (EF 1-12)
Challenge
The supersmart elves Atto and Bilbo have a big bar of chocolate with n columns and m rows, where m and n are positive integers. We denote by (i,j) the piece in the i -th column and the j -th row of the chocolate. The piece (n,m) is filled with orange jelly and is therefore disgusting (this fact need not be proved).
Atto and Bilbo play the following game: starting with Atto, they take turns making moves. A move consists of choosing a piece (i,j) that is still available and eat up all the pieces (i',j') with i'\le i and j'\le j . Whoever has to eat the piece (n,m) with the orange jelly loses.
Example: A possible move for n=7 and m=4 might look like this. If a player chooses the piece (4,2) in his turn, he must eat the pieces shaded in blue:
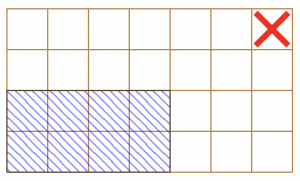
The piece (7,4) with the orange jelly is marked with a red X. In this example, a game, which Atto loses in the end, could look like this (see Figure 1):
- Atto (blue) starts with the piece (4,2) .
- Then, Bilbo (orange) chooses the piece (3,4) .
- Now, Atto chooses (6,4) .
- After that, Bilbo chooses (7,3) .
- Finally, Atto must eat the piece (7,4) with the orange jelly in his last move.

Figure 1: A possible game with a chocolate bar of size 7 \times 4 .
Depending on m and n , there is either a strategy that can guarantee a win for Atto, or a strategy that can guarantee a win for Bilbo.
If we choose m and n independently and randomly from the set \lbrace 1,2,3,\dots, 10^6\rbrace , all numbers being chosen with equal probability, what is the probability p that Atto has a winning strategy?
Possible answers:
- p<10\%
- 10\%\le p<20\%
- 20\%\le p<30\%
- 30\%\le p<40\%
- 40\%\le p<50\%
- 50\%\le p<60\%
- 60\%\le p<70\%
- 70\%\le p<80\%
- 80\%\le p<90\%
- 90\%\le p\le 100\%
Project reference:
In the project EF 1-12 Learning Extremal Structures in Combinatorics, we use approaches from the field of artificial intelligence and machine learning to find new structures with certain properties. This also helps us to find new winning strategies for combinatorial games, quite similar to the one from this task.