
© Friederike Hofmann, MATH+
Autor*innen: Olaf Parczyk, Silas Rathke (FU Berlin)
Projekt: Learning Extremal Structures in Combinatorics (EF 1-12)
Aufgabe
Die Intelligenzwichtel Atto und Bilbo haben sich eine große Tafel Schokolade mit n Spalten und m Zeilen besorgt, wobei m und n positive ganze Zahlen sind. Mit (i,j) bezeichnen wir das Stückchen in der i -ten Spalte und der j -ten Zeile der Schokolade. Das Stückchen (n,m) ist mit Orangengelee gefüllt und somit ekelhaft (diese Tatsache muss nicht bewiesen werden).
Atto und Bilbo spielen nun folgendes Spiel: Sie machen abwechselnd Züge, wobei Atto beginnt. Ein Zug besteht darin, ein noch vorhandenes Stück (i,j) auszuwählen und alle Stückchen (i',j') mit i'\le i und j'\le j aufzuessen. Wer das Stückchen (n,m) mit dem Orangengelee essen muss, der verliert.
Beispiel: Ein möglicher Zug für n=7 und m=4 könnte wie folgt aussehen. Wenn ein Spieler in seinem Zug das Stückchen (4,2) aussucht, muss er die blau schraffierten Stückchen essen:
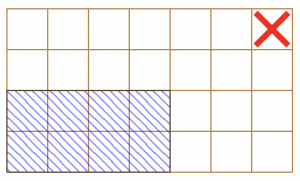
Das Stückchen (7,4) mit dem Orangengelee ist mit einem roten X markiert. In diesem Beispiel könnte ein Spielverlauf, bei dem Atto am Ende verliert, also möglicherweise wie folgt aussehen (siehe Abbildung 1):
- Atto (blau) startet mit dem Stückchen (4,2) .
- Anschließend wählt Bilbo (orange) das Stückchen (3,4) .
- Nun wählt Atto (6,4) .
- Danach sucht sich Bilbo (7,3) aus.
- Schließlich muss Atto in seinem letzten Zug das Stückchen (7,4) mit dem Orangengelee essen.

Abbildung 1: Ein möglicher Spielverlauf bei einer Tafel der Größe 7 \times 4 .
Abhängig von m und n gibt es entweder eine Strategie, mit der Atto sicher gewinnen kann, oder eine Strategie, mit der Bilbo sicher gewinnen kann.
Wenn wir m und n unabhängig und zufällig aus der Menge \lbrace 1,2,3,\dots, 10^6\rbrace wählen, wobei alle Zahlen mit der gleichen Wahrscheinlichkeit gewählt werden, wie hoch ist dann die Wahrscheinlichkeit p , dass Atto eine Gewinnstrategie besitzt?
Antwortmöglichkeiten:
- p<10\%
- 10\%\le p<20\%
- 20\%\le p<30\%
- 30\%\le p<40\%
- 40\%\le p<50\%
- 50\%\le p<60\%
- 60\%\le p<70\%
- 70\%\le p<80\%
- 80\%\le p<90\%
- 90\%\le p\le 100\%
Projektbezug:
Im Projekt EF 1-12 Learning Extremal Structures in Combinatorics verwenden wir Ansätze aus dem Bereich der künstlichen Intelligenz und des maschinellen Lernens um neue Strukturen mit bestimmten Eigenschaften zu finden. Dies hilft uns auch dabei neue Gewinnstrategien für kombinatorische Spiele zu finden, ganz ähnlich zu dem aus dieser Aufgabe.