Skip to content

20 Thieves in the Snow

© Friederike Hofmann, MATH+

Author:  Maximilian Stahlberg (TU Berlin)
Project: Evolution Models for Historical Networks (MATH+ Emerging Field Project EF5-6)

Challenge

The snowperson’s face is gone! Their cucumber eyes as well as their carrot nose have been stolen this morning. The pixies suspect that the culprits are to be found among the animals living close to the field, as it would not be the first time that they fail to resist the temptation of vegetables not meant for them. Immediately, an investigation is launched to solve the crime and confront the ravenous thieves.

At a first hearing, the little rabbit, the fawn, and the beaver claim that the carrot was firmly stuck in the snowperson’s face, but that the cucumber slices were already missing when they were going to school and work. The cat and the squirrel insist that they saw the snowperson only from a distance and that the carrot was in place, but that they were unsure about the cucumber eyes’ condition.

After this initial collection of evidence, the pixies are certain that the animals were all on the move one after the other—at least that explains the lack of witness reports… Moreover, the first animal passing the snowperson this morning seized the early moment and stole the cucumber slices, whereas the last animal passing by the faceless victim must have taken the carrot. Presumeably, they overslept and were sure that no one would witness the crime. Just one thing stands in the way of solving the crime: the pixies do not know who was first and who was last, since the animals were smart enough not to state particularly early or late departure times.

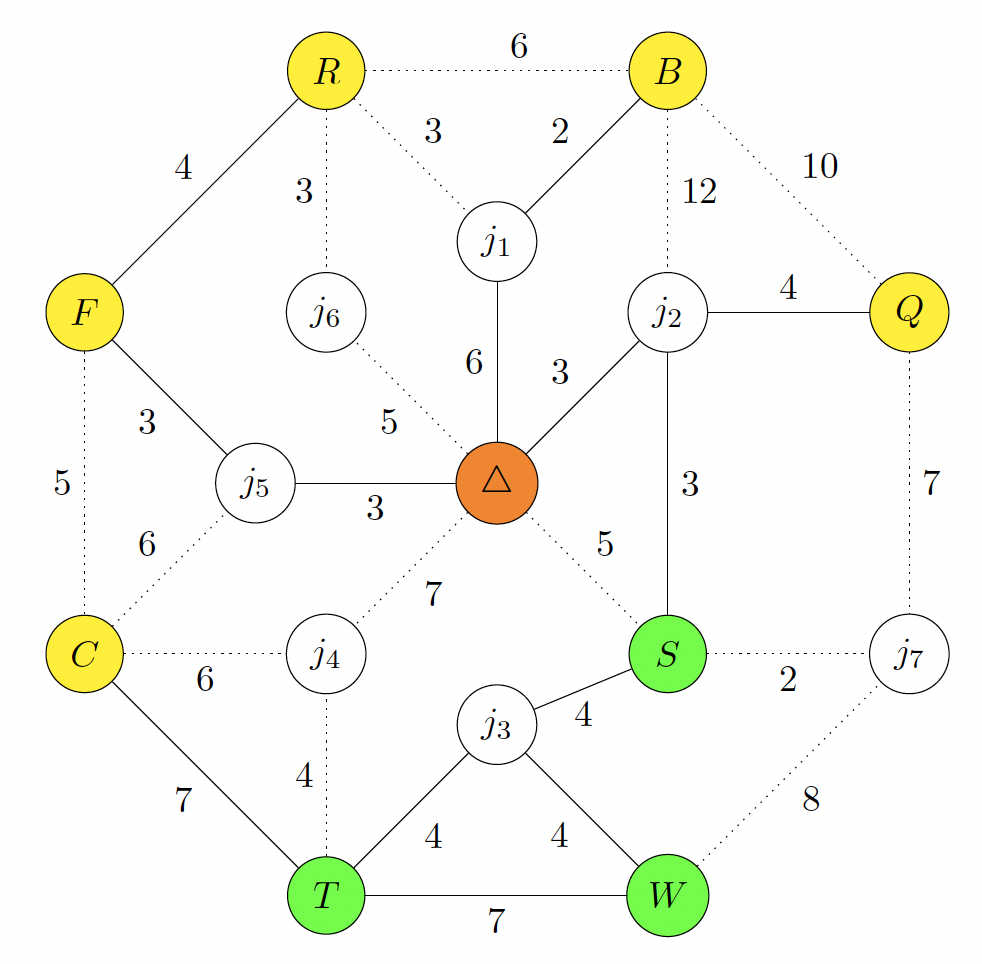
But the scout pixie Masha has an idea: while the tracks in the deep snow are already buried under a thin layer of fresh snow, revealing no incriminating paw prints, the principal corridors of movement of all the animals are still easy to recognize. Moreover, Masha knows that the animals have a very hard time plowing through fresh snow and prefer paths that have already been cleared by someone else. More precisely, she estimates that the time it takes the animals to traverse a cleared path segment is proportional to the length of that segment. However, traversing path segments with fresh snow takes them twice as long. Masha is also certain that the animals would always take the fastest route to their destination. In addition, all the animals can overlook the entire field and therefore see, even from a distance, which paths have already been cleared. Convinced by Masha’s theory, the pixies walk the crime scene and make a map:

Figure 1: The map of the crime scene shows the homes of the five animals (yellow), their daily destinations (green), the snowperson (orange), and the junction points (white). Solid lines mark cleared paths, dotted lines mark unused routes. Every path segment is labelled with its length in meters.

The pixies know that the little rabbit R and the fawn F still go to the school S, whereas the squirrel Q goes on a walk to the big tree T every morning. Both the cat C and the beaver B work in the wood workshop W. (The cat is very well known for her pretty scratch patterns.) The snowperson Δ stands in the middle of the large field, where many animals could have passed them this morning.

After a thorough analysis of the snow path network, Masha is certain that she has determined the precise order in which the animals have traversed the field today. She also knows who has eaten from the snowperson’s face.

Which of the following ten statements is correct?

Possible answers:

  1. The squirrel was on its way first and stole the cucumber slices. The beaver came last and ate the carrot.
  2. The fawn was first, but the beaver ate the cucumber slices. The rabbit could not resist the temptation of the carrot.
  3. The cat was first, but the fawn ate the cucumber slices. The beaver stole the carrot.
  4. The cat came first and stole the cucumber slices. The beaver ate the carrot.
  5. The squirrel was first, but the fawn stole the cucumber eyes. The rabbit ate the carrot. Everyone knows it’s his favourite vegetable!
  6. The cat was first, but the beaver stole the cucumber eyes. It should come to no surprise that the rabbit laid teeth on the carrot.
  7. The squirrel was first, but the fawn ate the cucumber slices. The beaver stole the carrot nose.
  8. The fawn was first and snatched the cucumber eyes. The beaver took the carrot.
  9. The beaver was first and stole the cucumber slices. The rabbit is the carrot thief.
  10. The fawn was first and snitched the cucumber slices. The rabbit came late to school and ate the carrot.
Challenge as PDF

Project reference:

The task at hand can get extremely hard for networks with a larger number of origin and destination pairs, because the number of possible orderings explodes. Already with five animals, there are a total of 5! = 120 possibilities to put their movement in a chronological order. In our research, we want to recover exactly such chronological orderings by analysing the network structure—except that, instead of cutting paths in the snow, we explore historical road networks, such as those built by the Romans. Also in this historical scenario it is often not clear which roads where constructed first. Furthermore, there may even be road segments that have not been discovered yet and are thus missing from our maps. But just as the animals preferred a path that has been cleared by someone else before them, later roads are expected to connect favourably to existing ones, since building new road segments was very expensive. By ordering assumed connections between ancient settlements, we try to reproduce the known road network and gain new insight into our ancient history.