
© Friederike Hofmann, MATH+
Author: Silas Rathke (FU Berlin)
Challenge
In the bar “At the Dripping Icicle”, Saint Nicholas is indulging in his favorite pastime: he talks incessantly about his house. What an architectural masterpiece it is! In its elegant simplicity, it combines the defining elements of Neo-Romanesque style with Scheldt Gothic! And despite this intellectual brilliance, every child still knows exactly what it looks like! Full of pride, he finally presents a drawing of his beloved house to his bored audience (see Figure 1).
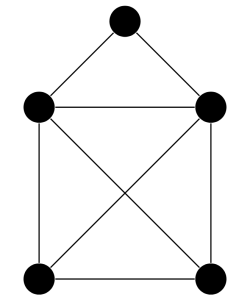
Figure 1: The House of Saint Nicholas consisting of five circles and eight connecting lines.
“And the best is yet to come!” he informs his unwilling audience. “Once you have drawn the five black circles, you can draw all eight lines between the circles without lifting your pen and without drawing any line twice!”
At this point, the mathematician elf Uhur has had enough and replies with one of his favorite sentences: “Prove it!”
Saint Nicholas freezes. After all, during his long-winded speech he has drunk one mulled wine or another, and now he simply cannot remember how to draw his house according to the rule mentioned above. He has no choice but to draw at random and hope for the best.
He pulls a thick red felt-tip pen out of his sack and decides to trace over the thin black lines in the drawing of the House of Saint Nicholas with the felt-tip pen.
To do this, he chooses one of the five circles uniformly at random (In this case, uniformly at random means that all circles are chosen with the same probability) as a starting point and places his pen there. From then on, he always draws the next line in the following way: he looks at where his pen currently is, checks which lines in the black drawing have this circle as an endpoint and have not yet been traced. From these, he chooses one uniformly at random and independently of his previous decisions, and traces it with the felt-tip pen. He continues in this manner until his pen reaches a point where all lines have already been traced in red.
Let p be the probability that he has then actually traced the complete Saint Nicholas House. What is the 100th digit after the decimal point in the decimal expansion of p?
Possible Answers
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 0