5 Sporty Lunch Break

© Julia Nurit Schönnagel, MATH+

Author: Thomas Nowotka (MATH+)

Challenge

Even at the North Pole, it is now recognized that physical activity is extremely beneficial for well-being and concentration. Therefore, it is mandatory for all employees of Santa’s workshop to participate in a shared movement game during the lunch break.

Today, the head elf Alvie is responsible for organizing the break.
He lines up in a circle with all the elves who are on shift today. At the beginning of the game, Alvie holds a magical ball made of stardust in his hand. This ball is now thrown back and forth over several rounds according to the following fixed rules:

1. The k-th round begins with Alvie passing the ball to the k-th colleague to his left.
2. In the k-th round, each elf who receives the ball throws it to the k-th elf to their left.
3. A round ends as soon as the ball has returned to Alvie.

Figure 1 shows, as an example, how the second and third rounds proceed when 8 elves are at work.

Alvie wants to pass the ball to each elf exactly once, therefore as many rounds are played as there are elves present excluding Alvie. Since the elves have a strong sense of justice, they cheer at the end of a round if every elf was able to throw the ball during that round. Figure 1 illustrates how the third round proceeds when 8 elves are at work. One can see that each elf gets to throw the ball once, so at the end of the third round they cheer.

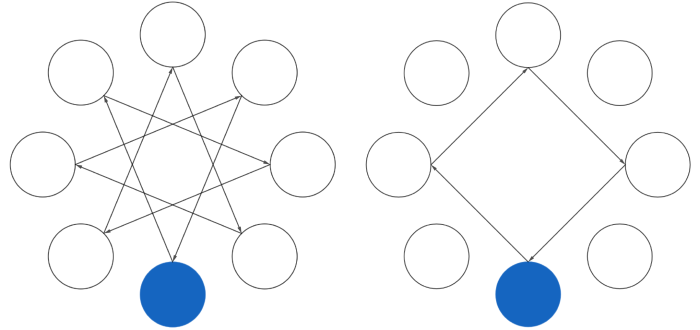
Figure 1: The third and the second round when 8 elves (circles) are at work. Throws are depicted as arrows. Alvie is shown in blue.

At the end of the day, when Alvie has to write a report for Santa, he realizes that he does not exactly remember how many elves, including himself, worked in the workshop today. After much thought, he can narrow it down to ten possibilities (see answer choices).  He also remembers that he heard 80 cheers during the lunch break today.

Can you tell Alvie how many elves (including him) were at work today?

Remark: It can be shown that, in every round of the game, the ball returns to Alvie after a finite number of throws. You may assume this for this problem.

Hint: Every positive integer greater than one can be written as a unique product of prime numbers (unique up to the order of the factors). This product is called prime factorization and may be helpful in solving this problem.

Possible Answers

1. 148
2. 151
3. 152
4. 157
5. 164
6. 166
7. 173
8. 179
9. 181
10. 184