23 Candy Presents

© Julia Schönnagel, MATH+

Author: Nikola Sadovek (FU Berlin)
Project: MATH+

Challenge

Santa is currently in the process of designing gifts for kids. Each gift should be made of one or more of the n types of candy, denoted as C_1, \dots , C_n . Santa is enthusiastic about creating unique gifts for each child and promoting the sharing of candies among them. To achieve this, Santa has asked for the help of the elves.

Specifically, the elves are tasked with designing the maximum number M of gifts, denoted as P_1, \dots, P_M , which will then be distributed to M kids, with each child receiving exactly one gift. The presents are defined by which of the n candy types C_1, \dots, C_n they contain and they should satisfy the following two conditions:

1. The uniqueness of the gifts is essential, and Santa requires that all presents be different. Two presents P_i and P_j are considered different if one of them contains a type of candy that the other one does not (although they are allowed to share some types of candy).
2. To encourage candy-sharing among the kids, Santa wishes that any combination of two presents should include all n candy types, C_1, \dots , C_n. This way, if any two kids decide to combine their gifts, they will have access to all the candy types. An example is illustrated in Figure 1 below.

 

 

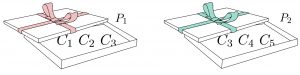
For n=5 presents P_1 and P_2 satisfy conditions (1) and (2).

What is the largest number M of presents P_1, \dots , P_M satisfying properties (1) and (2) that the elves can design?

Remark: Empty presents count as presents.

Possible Answers

1. 3
2. 4
3. n
4. n+1
5. \frac{n(n-1)}{2}
6. \frac{n(n-1)}{2} + 1
7. n^2
8. n^2+1
9. 2^{n-1}
10. 2^{n-1}+1