
© Christoph Graczyk, MATH+
Authors: Olaf Parczyk, Silas Rathke (FU Berlin)
Project: Learning Extremal Structures in Combinatorics (EF 1-12)
Challenge
This year, the Women’s Ice Soccer World Cup is held at the South Pole. However, ice-soccer is not played as often in “Down Under” as at the North Pole. That’s why the ice-soccer stadiums are a little outdated.
Martina, the stadium manager, experienced this first-hand: as she walked across the ice-soccer field, she collapsed immediately into the ice. After drying her feet and recovering from the shock, she decides to test the entire ice-soccer field to know whether the ice is also unstable at other spots.
To do this, she divides the field into a 4\,\times\,9 grid as follows:
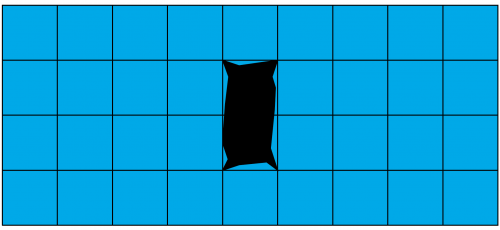
Figure 1: The 4 \times 9 ice-soccer field with Martina’s break-in point.
The two squares in the middle mark the point where she broke into the ice. She can no longer enter these two squares. However, she now wants to test all the other squares for stability.
To do this, she wants to start at any square of the soccer field and step on as many squares as possible, one after the other, without ever leaving the field. She is also not allowed to step on a square that she has already visited before. Only at the end she wants to return to the square where she started. But this is the only exception where a square can be entered twice. (Author’s note: I don’t know why she came up with these crazy rules. This story was passed from the South Pole to Germany and it may well be that some details have changed over time.)
To make matters worse, she limps after having fallen into the ice. This means that she has to alternate between a long and a short step. With a long step, she has to walk to a square which is in chess a “knight move” away. As illustrated in Figure 2, after a long step, Martina ends up on a square that is two steps horizontally and one step vertically, or two steps vertically and one step horizontally away. (Author’s note: At this point, the critical reader may ask whether the ice-soccer field is really so small that you can get from a square on the far left to a square on the far right with only four long steps. Yes, it is. And again, unfortunately, I don’t know why that is the case. As I said, this story has been told so many times that the details may have changed…)
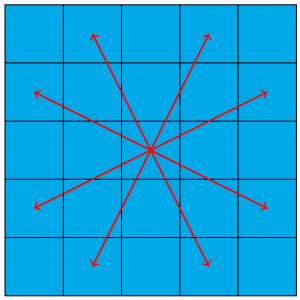
Figure 2: All possibilities for a long step starting in the central square.
With a short step, she must move to a horizontally or vertically adjacent square, as illustrated in Figure 3.
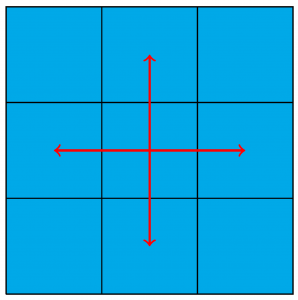
Figure 3: All possibilities for a short step starting in the central square.
A possible sequence of steps could look as in Figure 4. In this sequence, she stepped on six squares.
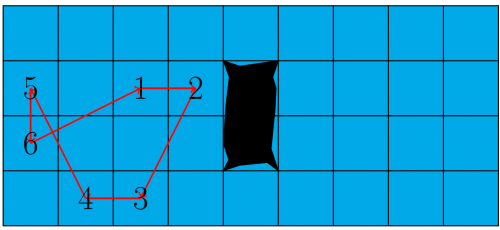
Figure 4: A possible path of Martina.
What is the largest number of squares she can visit in a one step-sequence?
All conditions summarized:
- The field has two holes that are not allowed to be stepped on.
- Martina chooses her starting field.
- She alternates between a long and a short step.
- She does not enter any square twice, except the starting square on which she ends her step-sequence.
Possible Answers
- 34
- 33
- 32
- 31
- 30
- 29
- 28
- 27
- 26
- Less than 26
Project Context
In the project “Learning Extremal Structures in Combinatorics” we use approaches from artificial intelligence and machine learning to find new constructions for graphs with certain properties.
The presented challenge can be formulated as an extremal problem in graph theory, similar to the problems we study in this project.