
© Vira Raichenko, MATH+
Authors: Hajo Broersma, Jesse van Rhijn (University of Twente)
Project: 4TU.AMI
Challenge
During their downtime, some of Santa’s elves like to play a game which they call “advanced tug-of-war”. In this game, the elves are divided into two (possibly unequally sized) teams, distinguished by yellow and blue hats. All participating elves stand in a circle and tie ropes to the other elves, such that each two elves are connected by one rope. Each team tries to pull the other team over to their side by tugging on the ropes.
The ropes used for this game can have one of two colors, red or green. However, the colors impose no restrictions on the game and can be chosen arbitrarily. A spectating elf notices that sometimes, especially when many elves participate, it happens that three elves from one team are among themselves all connected by ropes of the same color. We call this a perfect triangle; see Figure 1 for an example.
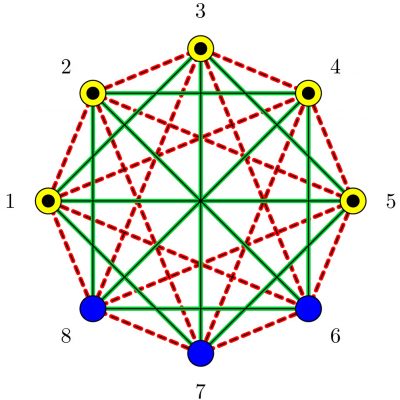
Figure 1: An example of an advanced tug-of-war game with eight elves. Green ropes are drawn as solid lines, red ropes are drawn as dashed lines. Blue dots represent elves with a blue hat, yellow dots (with a black central dot) represent elves with a yellow hat. Elves 1, 3 and 5 form a perfect triangle: they are pairwise connected by green ropes, and each of them wears a yellow hat.
What is the smallest number of elves that must participate in advanced tug-of-war in order to guarantee that there is a perfect triangle?
Possible Answers
- Six elves.
- Seven elves.
- Eight elves.
- Nine elves.
- Ten elves.
- Eleven elves.
- Twelve elves.
- Thirteen elves.
- Fourteen elves.
- There is no such number (we can always assign colors to avoid a perfect triangle).