
© Friederike Hofmann, MATH+
Author: Lukas Protz (MATH+)
Challenge
To relieve the elves from coloring gift boxes in the shape of a cube, the eager elf Eifi has purchased a machine. This machine is intended to take over the coloring process for the elves. As eager as Eifi is, he has already had all the lids for the gift boxes made by the machine. They are all colored with yellow stars on a dark blue background.
Unfortunately, Eifi forgot to ask Santa Claus beforehand if the elves are even allowed to use the machine. Santa is not thrilled that all the gift box lids look the same. In order to quickly find the right gift when distributing them on Christmas, he would prefer that all the gifts look different. He also finds colorful gifts much more beautiful than monochrome ones.
Eifi tries to reassure Santa by showing him that the machine can randomly color each of the remaining five sides of a gift. There are even nine different colors available for coloring.
Santa Claus, however, is not convinced of that. It could still happen that a present is colored in only one or two colors. Therefore, he makes Eifi an offer. Initially, he must ascertain the variety of distinct color combinations achievable for the gift, excluding the lid, by employing the nine available colors. Two presents are considered differently colored if they differ not solely by reflections or rotations. Let a be the proportion of all colorings such that the number of sides which have the same color as some other side is at most two. The elves are allowed to use the machine if the proportion a is greater than 0.7. Otherwise, they must, as always, color all the presents themselves so that all sides always have different colors. What is the proportion a of presents with at most two identically colored sides?



Figure 1: A present already wrapped. Top left: The present from one side, top right: The same present from the opposite side, bottom: The net of the present without the lid.
Explaination of reflection and rotation
To explain the concept of reflection we are considering two 2\times 4 grids as shown below:
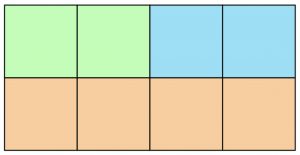
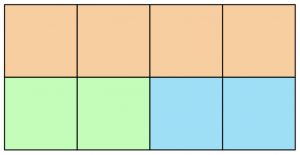
These two grids are not different, as they only differ by a horizontal reflection between the two rows.
To explain the concept of rotation we are again considering two 2\times 4 grids as shown below:

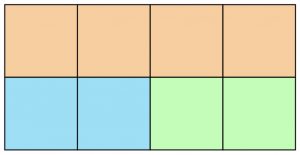
These two grids are not different, as they only differ by a rotation of \pi (or 180^\circ).
Possible Answers
- a \le 0.1
- 0.1 < a \le 0.2
- 0.2 < a \le 0.3
- 0.3 < a \le 0.4
- 0.4 < a \le 0.5
- 0.5 < a \le 0.6
- 0.6 < a \le 0.7
- 0.7 < a \le 0.8
- 0.8 < a \le 0.9
- 0.9 < a