
© Vira Raichenko, MATH+
Author: Wouter Fokkema (4TU.AMI)
Challenge
Santa has too little space to store all his presents! Luckily, he found an old basement that still has some room. The basement is divided into cells. A top view of the basement is shown below. Santa wants to store as many presents in the basement as possible.
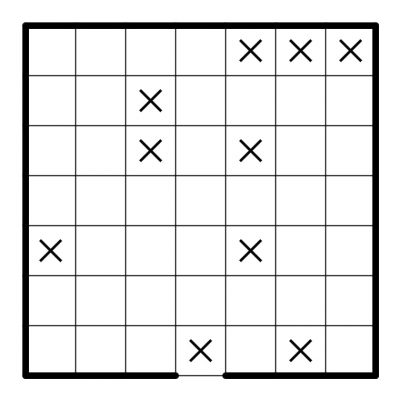
Figure 1: The layout of Santa’s basement. The cross in the center of the bottom row marks the entrance. All other crosses mark places, where the ceiling leaks.
However, there are some rules:
- A present takes up exactly 1 cell.
- No presents are allowed at the entrance and in places where the ceiling leaks; these cells are indicated with a cross.
- 2 presents may not be in horizontally or vertically adjacent cells. (This is, because all presents look similar and two presents next to each other can easily be confused.)
- Starting from the entrance to the basement, it must be possible to visit every cell without a present by moving horizontally and vertically through cells without presents. In other words, the cells that do not contain a present (including the cells with a cross) must form 1 area of cells that is connected orthogonally. (This is important, because the presents have to be inspected regularly. Thus it would be additional work, if one needs to move them around.)
Santa needs your help determining the maximum number of presents that can fit in the basement. What is that maximum number?
Possible Answers
- Eleven presents
- Twelve presents
- Thirteen presents
- Fourteen presents
- Fifteen presents
- Sixteen presents
- Seventeen presents
- Eighteen presents
- Nineteen presents
- Twenty presents