
© Zyanya Santuario, MATH+
Author: Matthew Maat (Universiteit Twente)
Project: Combining algorithms for parity games and linear programming
Challenge
After consulting with king Herod, the wise men are getting ready to travel to Bethlehem from Jerusalem. There is only one problem that they would like to solve before leaving: taxes. Because of the large amount of gold and spices they carry, they will have to pay taxes in every town that they enter. To make things worse, those smart tax collectors have pointed all road signs towards the places where you need to pay the most taxes. On the map ( g. 1) you see the roads and towns between Jerusalem and Bethlehem represented by arrows and circles respectively, and how much tax the men need to pay in every town. In red, you see the directions of the signs in the towns.
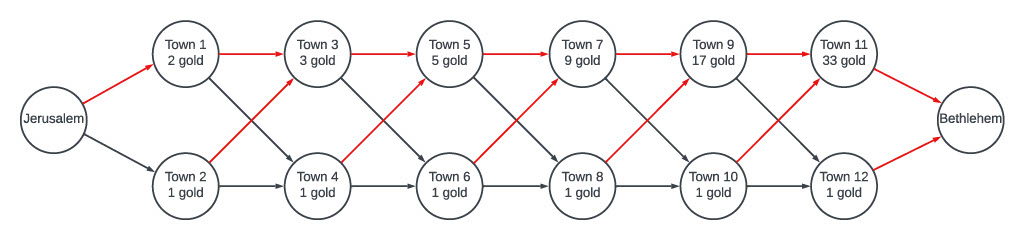
Figure 1: The roads (arrows) from Jerusalem to Bethlehem, with the amount of tax written in the circles. The caravan can only travel in the direction of the arrows.
The men decide to send Balthasar forward with the following assignment:
- Starting from Jerusalem, walk to Town 1, then Town 2, 3, etc. Since Balthasar is on foot, he may ignore all the roads that exist.
- If Balthasar is in a town where he can change the sign such that the trip from that town to Betlehem becomes cheaper, then he changes the sign, runs back to Jerusalem, and starts the whole process over.
- If Balthasar changes the sign, he may only point the signs following the direction of the arrows of the roads. For example, in Town 7, the sign can only point towards Town 9 or Town 10.
- If Balthasar reaches Bethlehem, he will send a carrier pigeon to let the others know that they can come to Bethlehem.
On his first trip, Balthasar changes the sign in Jerusalem towards Town 2, since then the total tax on the trip from Jerusalem becomes 1 + 3 + 5 + 9 + 17 + 33 instead of 2 + 3 + 5 + 9 + 17 + 33 gold pieces. Likewise, on his second trip, Balthasar will switch the sign in Town 1 towards Town 4. On his third trip, he changes the sign in Jerusalem back to Town 1. This is, because the trip from there to Bethlehem becomes cheaper. Indeed, the new trip costs 2 + 1 + 5 + 9 + 17 + 33 which is cheaper than the cost 1 + 3 + 5 + 9 + 17 + 33 of the old trip.
How many times will Balthasar change a sign in total? (if the sign is changed in a town multiple times, we count it multiple times)
Answer Options
- 55
- 57
- 63
- 83
- 114
- 120
- 126
- 177
- 240
- 367
Project Context
The algorithm that Balthasar uses is called the strategy improvement algorithm. The algorithm uses a so-called improvement rule that decides in which order we make improvements (or in which order Balthasar visits the towns). In this case we use what is called Bland’s rule. Although this is a one-player game (we only minimize the price), we can also use the algorithm when there are towns controlled by a maximizer or a random player. It is unknown whether there is an improvement rule that guarantees a small number of iterations. As you can see, even with a small number of towns, Bland’s rule can take a large number of iterations.