
© Zyanya Santuario, MATH+
Author: Dion Gijswijt (TU Delft)
Project: 4TU.AMI
Challenge
Presently, Santa is on a mission to deliver gifts to children. His journey spans six cities, denoted as A to F. Starting from Santa’s Workshop (SW), he must select one among A, B, C, D, E, or F to begin his visit.
The reindeers, tired from playing, can’t travel long distances anymore. This necessitates Santa to chart the shortest route possible. He has a map, which indicates flying distances between cities along connecting lines, and the circles display the distances from SW to each city.
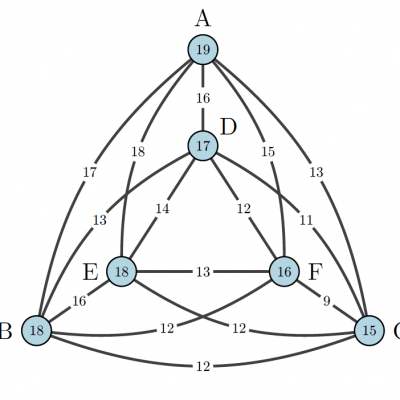
Santa has to choose now the shortest sequence for visiting the cities before returning to Santa’s Workshop. For instance, if he takes the route SW-F-A-E-B-C-D-SW, the total journey length adds up to 16+15+18+16+12+11+17=105.
What is the length of the shortest tour that Santa can take?
Possible Answers:
- 104
- 103
- 102
- 101
- 100
- 99
- 98
- 97
- 96
- 95