
© Vira Raichenko, MATH+
Author: Matthew Maat (Universiteit Twente)
Project: Combining algorithms for parity games and linear programming
Challenge
During their long journey through the desert, the wise men have fallen asleep while riding their camels. Upon waking up they are surprised, as they cannot see the star anymore. In fact, the whole sky is covered in a big cloud. This must be the infamous cloud of Al-Bermuda. A legend says that it is shaped like an isosceles right triangle, with its longest side being 100 miles long. It is not possible to orient as long as they are under the cloud. But once they manage to get out from under the cloud, they will notice immediately because they will see the star again. Unfortunately, they have hardly any water left, so the sooner they can escape the cloud the better. There’s only enough for 100 miles. Caspar bets Melchior that he can guarantee they will escape the cloud with less than 100 miles of walking if they follow his lead, so that hopefully they won’t become thirsty.
Caspar starts to think about his strategy. If he just walks in a straight line for 100 miles, it is possible that they are now in the lower left corner of the triangle, and that they happen to walk exactly to the right (see line segment AB in Figure 1). Then they don’t escape within 100 miles. Instead, if he walks in a circle with a circumference of 100 miles, it is possible that they started in point C (see Figure 1) and don’t leave the triangle during the 100 miles of walking. After some more thinking, he comes up with 4 more strategies (see also Figure 1):
(a) Walk straight for 50 miles, then take a turn of size \alpha, and walk straight for 50 more miles.
(b) Walk straight for x miles, take a 90^\circ turn to the right, then walk straight for 100-2x miles, then another right, and then another x miles straight.
(c) The same as (b), but now at the second turn we turn left instead of right.
(d) Walk straight for z miles, and then turn right and walk straight for another 100 - z miles.
Assuming Caspar picks the right values for parameters \alpha, x, y and z if they exist, which of these strategies can Caspar use to guarantee himself to win the bet?
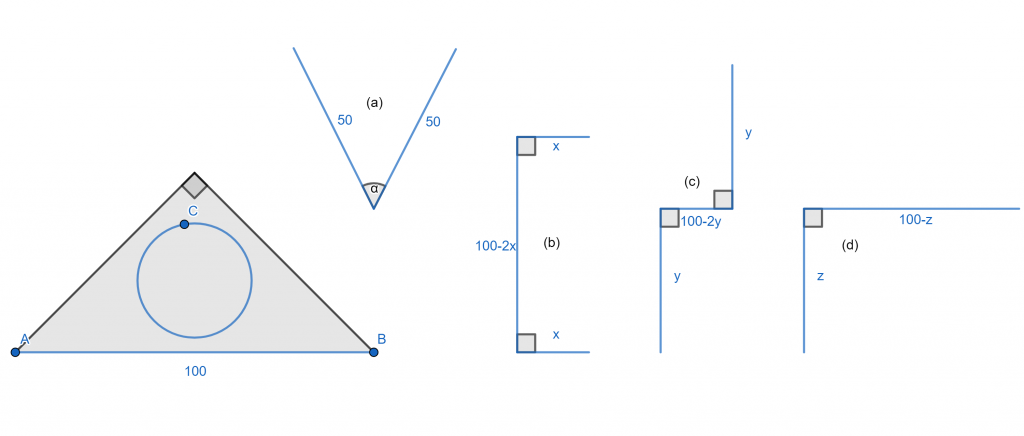
Figure 1: Left: the triangle of Al-Bermuda. Right: Caspar’s ideas for the routes to take.
Possible Answers
- Caspar cannot guarantee the win
- Only one of the four strategies
- Only with (a) and (b)
- Only with (a) and (c)
- Only with (a) and (d)
- Only with (b) and (c)
- Only with (b) and (d)
- Only with (c) and (d)
- Three of the four strategies
- Caspar can guarantee to win with all four strategies