
© Ivana Martic, MATH+
Authors: EWM-NL
Challenge
Julia Robinson was one of the best female mathematicians of the 20th century, and is an old friend of Santa. She worked on the so-called Hilbert’s 10th problem, but also worked on game theory. Now, Santa needs her help with a funny game that his elves have created to have some fun while working on an assembly line.
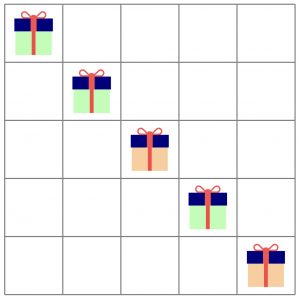
Figure 1: The assembly process for n=5.
Santa is packaging and sending presents, with n assembly lines. The assembly process is an n × n square grid, and all n packages are on the diagonal of this square, see Figure 1. To be able to send them away, these packages need to be transported to the lowest row of the square. To do so, Santa’s elves can move the presents downward. However, they can only do this by moving two packages at the same time downward by one step. Packages at the bottom row cannot be moved any further, as otherwise they would fall off the assembly line.
Santa would like to end up with the lowest row full of all the n presents (so that all packages can be sent). However, sometimes his elves seem to get stuck and not be able to send all presents. When is it possible for Santa to get all his presents to the bottom of the assembly square with some algorithm at all and not be stuck?
Answer Options:
- For every possible value of n
- For n even
- For n odd
- For all n \ge 24
- For all n \ge 12
- For all n where either n-1 or n are a multiple of 4
- For all n where either n+1 or n are a multiple of 4
- For all n where either n-1 or n are a multiple of 3
- For all n where either n+1 or n are a multiple of 3
- For no value of n
Project Context:
EWM-NL is the Dutch association for women in mathematics.