
© Julia Nurit Schönnagel, MATH+
Author: Attila Karsai (TU Berlin)
Project: Structured optimal control of port-Hamiltonian network models (CRC/TRR 154, Project B03)
Challenge
Santa’s little helper Ruprecht was given an important task this year. He is responsible for supplying the cities A , B , and C with presents. Figure 1 shows the arrangement of the cities, which all lie on a straight line heading east. The cities A and B are 5 kilometers apart, the cities B and C even 15 kilometers.
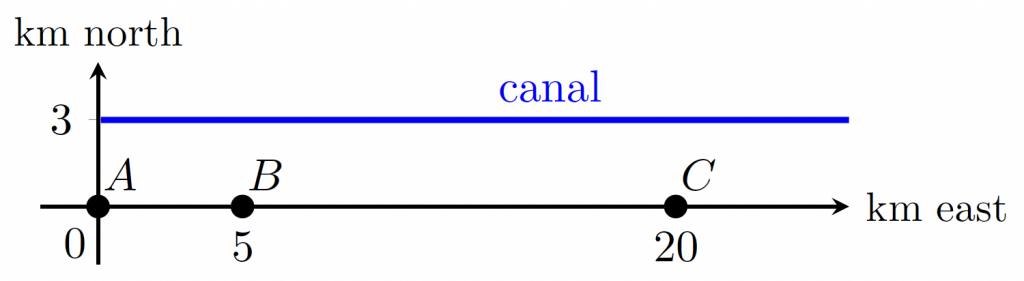
Figure 1: Arrangement of the cities and the frozen canal.
Ruprecht just finished supplying city A with presents and wants to impress Santa by delivering the cities B and C as quickly as possible. Unfortunately, there was heavy snowfall last night, and the streets connecting the cities are buried under a thick layer of snow. Therefore, Ruprecht’s progress is much slower than before. However, from earlier visits to this region, Ruprecht remembers that 3 kilometers north of A there is a canal that runs straight east. Figure 1 also shows this canal. Because of the freezing temperatures, the canal is frozen right now, and Ruprecht can ice-skate on the surface of the canal.
When Ruprecht trudges through the thick layer of snow, he manages to cover 5 kilometers per hour. On the frozen canal, with the help of his skates, he proceeds at 25 kilometers per hour.
We have the following questions:
- Does Ruprecht use the frozen canal on the fastest way from A to B ?
- Does Ruprecht use the frozen canal on the fastest way from B to C ?
- Does Ruprecht need more than 1 hour for the fastest way from A to B ?
- Does Ruprecht need less than 1.8 hours for the fastest way from B to C ?
Possible answers:
- (a) no, (b) no, (c) no, (d) no.
- (a) no, (b) no, (c) no, (d) yes.
- (a) no, (b) no, (c) yes, (d) no.
- (a) no, (b) no, (c) yes, (d) yes.
- (a) no, (b) yes, (c) no, (d) no.
- (a) no, (b) yes, (c) no, (d) yes.
- (a) no, (b) yes, (c) yes, (d) no.
- (a) no, (b) yes, (c) yes, (d) yes.
- (a) yes, (b) yes, (c) no, (d) no.
- (a) yes, (b) yes, (c) no, (d) yes.
Project reference:
A branch of mathematical optimisation is concerned with optimal control problems. Such control problems arise in a variety of real-world applications, ranging from economics over robotics to the control of the power grid of a whole country. In many cases, it can be observed that the optimal control requires a detour to reduce costs. This phenomenon is called turnpike phenomenon. The name is reminiscent of an observation from everyday life: when driving a long distance, it is almost always quicker to take a detour via a freeway (turnpike) than to drive slowly on the country road all the time.