
© Zyanya Santuario, MATH+
Author: Matthew Maat (Universiteit Twente)
Project: Combining algorithms for parity games & linear programming
Challenge
It seems like any other night. A small group of shepherds is sitting by a fire. The last rays of sunshine slowly get replaced by the light of a bright star in the middle of the sky. Unaware of what they would witness later that night, the men try to fall asleep.
As every shepherd knows, the best way to fall asleep is to count sheep. However, as they do this every night, they want to have some fun and try to arrange the sheep in a vertical sheep-conga, which we will define iteratively.
A vertical 1-sheep conga consists of just one sheep. Larger vertical sheep-congas can be constructed from smaller ones. In the following construction, sheep are idealized and represented as circles. For any integer n>1, a vertical n-sheep-conga consists of one vertical (n-1)-sheep-conga and two identical horizontal \lceil \frac{n}{2}\rceil-sheep-congas (see footnote for \lceil x\rceil), where a horizontal sheep-conga is simply a vertical sheep-conga rotated by 90 degrees. The two horizontal sheep-congas are placed above and below the vertical sheep-conga and centered on the same vertical line, so that the final figure has both a horizontal and a vertical axis of symmetry.
In Figure 1 you can see some examples of vertical sheep-congas. The brown sheep represent the vertical (n-1)-sheep-conga and the white sheep represent the horizontal \lceil \frac{n}{2}\rceil-sheep-conga of the respective n-sheep-conga.
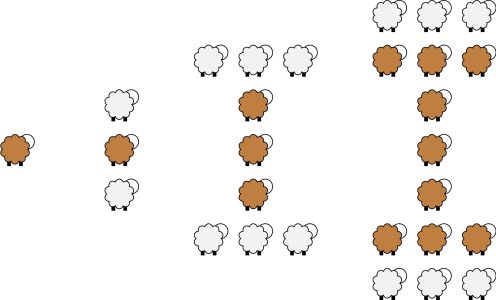
Figure 1: From left to right: a 1-sheep-conga, a 2-sheep-conga, a 3-sheep-conga and a 4-sheep-conga.
If C is the number of sheep in a (2025^5)-sheep-conga, which of the following statements is true?
Footnote: \lceil x\rceil means the smallest integer that is at least as big as x, for example \lceil 6.5 \rceil =7=\lceil 7 \rceil
Possible Answers:
- C\leq 2025^5
- 2025^5<C\leq 2025^{20.25}
- 2025^{20.25} < C \leq 10^{100}
- 10^{100} < C \leq 10^{202.5}
- 10^{202.5}<C\leq 2.025^{2025}
- 2.025^{2025}<C \leq 5.202^{2025}
- 5.202^{2025}<C\leq 20.25^{2025}
- 20.25^{2025}<C\leq 2025!
- 2025!< C \leq \left(2025^5\right)^{2025^5}
- C>\left(2025^5\right)^{2025^5}