15 The Road from Bethlehem

© Julia Nurit Schönnagel, MATH+

Author: Matthew Maat (Universiteit Twente)
Project: Combining algorithms for parity games & linear programming

Challenge

After the visit of the shepherds and the wise men, Joseph is warned in a dream: he, his wife Mary and the baby Jesus must flee to Egypt to escape from the evil king Herod (Book of Matthew, chapter 2, verse 13-15). However, reaching Egypt from Bethlehem is not without peril. Because they do not know the way, they will have to trust in the directions of locals that they meet on their journey. Most of all, they hope to avoid Roman checkpoints where they will surely get caught.

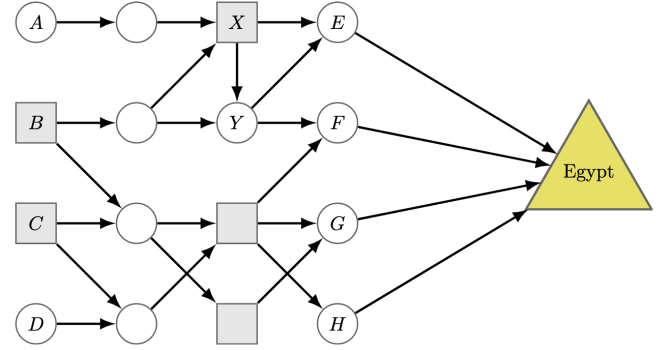
Figure 1: The road map. Circles and squares are cities. Arrows are one-way roads between cities, which can only be used in the direction given by the corresponding arrow.

The road network is shown in Figure 1. Maria and Joseph start in Bethlehem (B on the map). The 16 cities are marked by squares and circles. Each of the cities Emmaüs, Filadelfia, Gerar and Hebron (E, F, G and H) may or may not contain a Roman checkpoint (there are no checkpoints in other cities than these four). It is common knowledge to everyone in this region what the map looks like and where the checkpoints are. However, people from this region do not trust strangers easily, so they will not reveal their whole geographical knowledge to travelers. Instead, whenever travelers arrive, the people from the city will tell them which road to take from their city. All roads are one-way, they can only be used in one direction, not the other, and it is not possible to turn around in the middle of the way. Since travelers do not know the way, they will always follow any directions given to them.

In most cities (white circles), people are friendly, and they will send travelers in a direction that will let them avoid the checkpoints, if possible. However, some cities (grey squares) are completely inhabited by spies of Herod: they will point any travelers in a direction that leads them to a checkpoint, if possible. The friendly people and the spies are also aware of where the spies are and, considering the whole journey till the end, choose one of the best options to reach their goals.

Example: Suppose that Emmaüs has a Roman checkpoint and Filadelfia does not. Then if any travelers arrive in city X, then the spies will direct them to E. Or if the travelers arrive in city Y, then the friendly inhabitants will send them to F. Note: the spies will not send travelers from X to Y in this case, as they know the friendly inhabitants would send travelers to F.

In the end, Joseph and Mary arrive safely in Egypt with the child, without encountering any checkpoints. In Egypt, they also meet other travelers that started in Afek, Caesarea and Damascus (A, C, D on the map) and were also dependent on recommendations from locals.
Strangely, all the other travelers had encountered Roman checkpoints on their journey to Egypt.
Given that Joseph and Mary did not encounter a Roman checkpoint and the other travelers did, which statement is true about the location(s) of the checkpoint(s)?

Note: Travelers are also given directions at their starting points.

Possible Answers

1. There is only one possibility for the distribution of the checkpoints, in which there is precisely one checkpoint.
2. There must be exactly two checkpoints, which must be in E and in F.
3. There must be exactly two checkpoints, which must be in E and in G.
4. There must be exactly two checkpoints, which must be in E and in H.
5. There must be exactly two checkpoints, which must be in F and in G.
6. There must be exactly two checkpoints, which must be in F and in H.
7. There must be exactly two checkpoints, which must be in G and in H.
8. There is only one possibility, in which there are precisely three checkpoints.
9. There are precisely two possible distributions of checkpoints.
10. There are more than two possible distributions of checkpoints.

Project Reference

This problem is related to reachability games.