11 Beautiful Gift-Wrapping Using a Spirograph

© Zyanya Santuario

Author: Eva Deinum (Wageningen University & Research)
Project:  4TU.AMI

Challenge

The elves use a Spirograph to decorate gift-wrapping papers for the Christmas presents. This Spirograph consists of a movable inner cogwheel with n teeth and a fixed outer ring with N teeth, where N>n. The inner cogwheel as well as the outer ring are circular. The teeth of the inner cogwheel and the outer ring fit perfectly into each other, so that the inner cogwheel is not able to slip between the teeth of the outer ring but can only be rolled along the outer ring. The inner cogwheel has an off-centered hole for a pen. In Figure 1, the Spirograph setup is shown on the left, and the hole for the pen is marked with a blue dot.

By rolling the inner cogwheel along the outer ring while pressing down the tip of the pen through the hole, the elves can draw closed curves like the purple curve shown in the left part of Figure 1. The closed curves are obtained by rolling the inner cogwheel until it eventually returns to its starting position (with also the hole for the pen returning to its staring position). The so created curves can have various kinds of symmetry and can also intersect with themselves, e.g. the purple curve shown in the left part of Figure 1 intersects with itself and has a so called 7-fold (rotational) symmetry. Here, an n-fold rotational symmetry is a rotation around the center of the outer ring by \frac{360^\circ}{n}, that maps the closed curve to itself. When the rotation corresponding to the symmetry is applied n times, it is just a 360^\circ rotation.

By choosing cogwheels and rings with different values of n and N, the elves can create different curves. In the right part of Figure 1, we show two more examples of curves that can be created using a Spirograph with different values of n and N; the top one has 7-fold symmetry and intersects with itself, the bottom one has 8-fold symmetry and doesn’t intersect with itself.

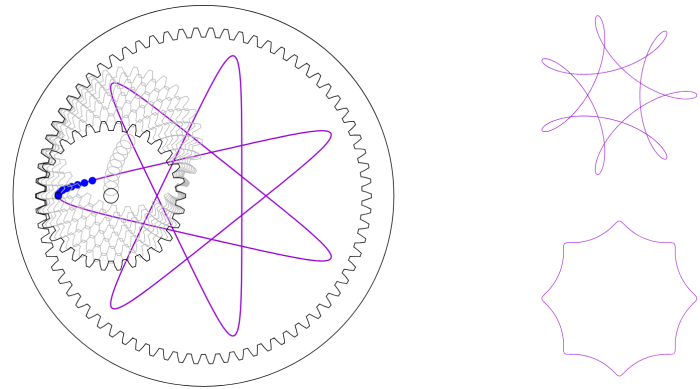
Figure 1: Spirograph setup (left), with in purple the curve it produces. Example of curves for other n, N values (right).

Today, a young elf is in charge of decorating the gift-wrapping paper. Unfortunately, he doesn’t fully understand the Spirograph yet and there are no other elves around to help him. He wants to make a curve that has the following two properties:

1. the curve has 5-fold symmetry;
2. the curve intersects with itself.

He can choose between three outer rings N=100, N=115 and N=144, respectively, as well as six inner cogwheels with n=20, n=23, n=36, n=40, n=46 and n=69, respectively. How many different combinations of outer ring and inner cogwheel can the young elf choose to draw a curve that has the two desired properties as mentioned above?

Possible answers:

1. 1 combination
2. 2 combinations
3. 3 combinations
4. 4 combinations
5. 5 combinations
6. 6 combinations
7. 7 combinations
8. 8 combinations
9. 9 combinations
10. Without knowing where the hole in the inner cogwheel is located, one cannot determine the number of combinations uniquely.