10 Christmas Light Show

© Ivana Martić, MATH+

An interactive tool for the challenge is available here.

Author: Lukas Protz (MATH+)

Challenge

The eager elf Eifi bought a lot of drones to help with all the work at the North Pole. Unfortunately, the elves at the IT department are not as eager as Eifi and tell him that they currently have no capacity to program the drones. Therefore, Eifi wants to program the drones himself. But not to help with the work – no, he wants to make a light show with the drones to entertain his fellow elves and help them relax and forget about the Christmas stress for a while.

Eifi has a few flight routes for the drones in mind. He introduces a coordinate system centered exactly at the North Pole. For simplicity, he assumes the area around the North Pole to be a perfect flat plane. The units of the coordinate system are the standard distance units at the North Pole, an elf-mile. The flight routes he has in mind depend on two positive integers a, b and can be parametrized by time in the following way:

\gamma(t) = (\sin(at),\sin(bt)),\quad 0\le t< 2\pi.

Note: For each value of t, the formula describes the two coordinates of the flight route at time t. Of course, the time t is measured in the standard time units at the North Pole, the elf-minute. Further, \sin(t) is a function w.r.t. (with respect to) arc length and not w.r.t. degrees, e.g. \sin(\pi) = 0 but \sin(180) \approx -0.8011 \neq 0.

Eager as Eifi is, he tries out a few combinations of a, b and lets the drones fly one after the other , but … oh no! For one of the combinations, at one point of the route, the drones start reversing their direction and travel back exactly the way they came from, thereby crashing into other drones. Eifi immediately stops his experiment. He wonders: For what combinations of a, b can this happen? Can you help Eifi figure out all pairs of a, b , where the drones start to travel back the path they came from at some point, so that he can continue his experiments to find the most beautiful flight route without causing accidents again?

Remark: For any real number \alpha, \sin(\alpha) is defined as the vertical coordinate of the point on the unit circle obtained by measuring an angle of \alpha radians counterclockwise from the intersection of the unit circle and the horizontal axis on the right side of the vertical axis. The unit circle is defined as the circle with radius 1, which is centered at the origin.
Figure 1 illustrates this definition and in Figure 2 the graph of the sine-function is shown for \alpha between -\pi and 3\pi.

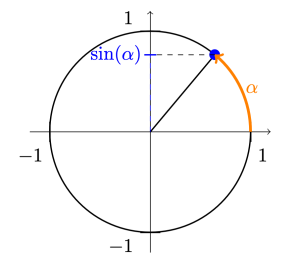
Figure 1: Illustration of the definition of \sin(\alpha).

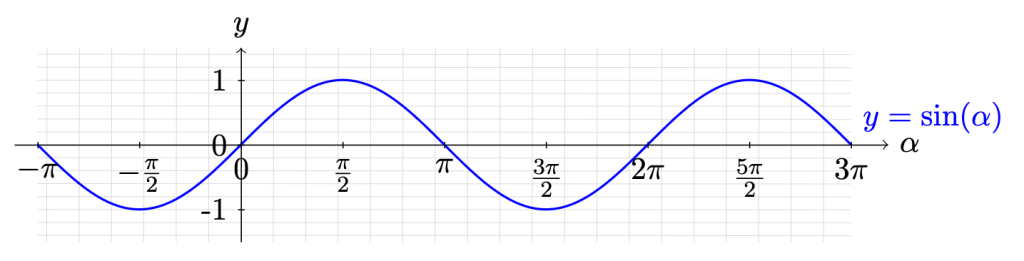
Figure 2: The graph of the sine-function.

Possible Answers

1. No combinations of a and b achieve this. Eifi just programmed the drones incorrectly.
2. There is exactly one combination of a and b and Eifi was just unlucky to have tested the drones with this combination.
3. There are only finitely many combinations of a and b that achieve this.
4. This can only happen if a=b.
5. This can only happen if a and b are coprime, i.e. have no common positive divisors other than the number 1.
6. This can only happen if a and b are not coprime, i.e. a and b do have a common divisor greater than 1.
7. This exactly happens if a and b are both powers of 2 or if a=b.
8. This happens exactly when the highest power of two dividing a is also  the highest power of two dividing b.
9. This happens for all combinations of a and b if both numbers are bigger than 2025^{2025}.
10. None of the other answers is true.