3 A Colorful Christmas

© Ivana Martić, MATH+

Author: Hajo Broersma

Project: 4TU.AMI

Challenge

Mondrian the painter-elf has designed a rectangular Christmas card as shown in Figure 1. The 8\times 12 area is divided into the following regions: 72 unit (1\times 1) squares, three 2\times 2 squares, and six 1\times 2 rectangles as shown.

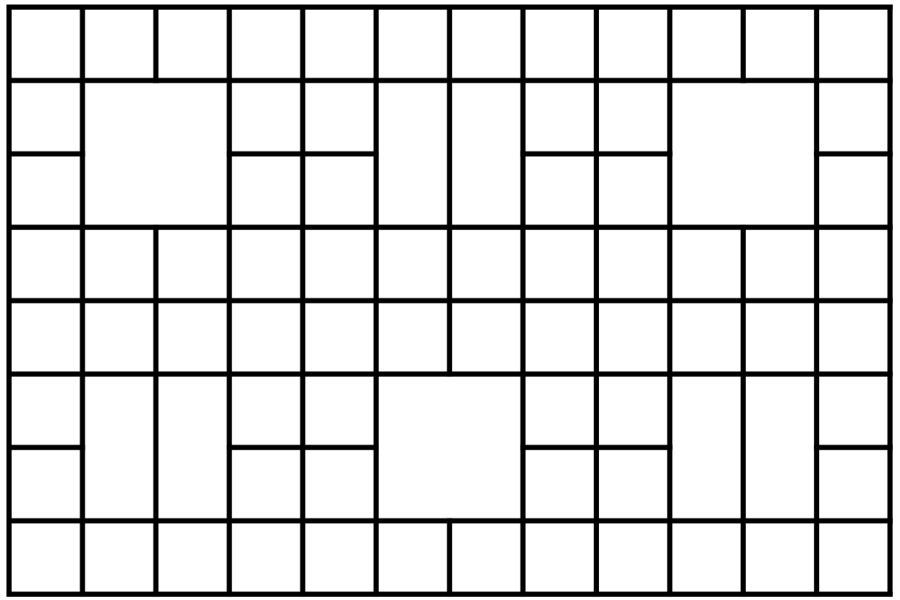
Figure 1: The uncolored Christmas card.

Mondrian asks three pixies to color all the different regions of the card with red, yellow and blue, such that each 1\times 1 unit square, each 2\times 2 square and each 1\times 2 rectangle receives one of these three colors. The completed coloring is called proper if regions of the same color share no line segment (though they may share a point); see Figure 2 for examples.

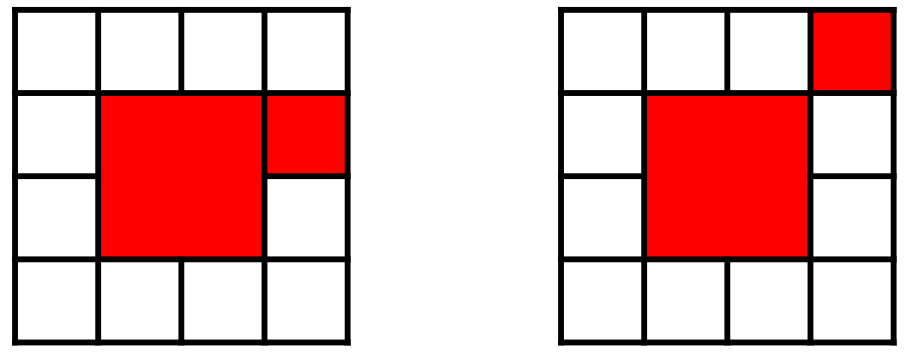
Figure 2: The (partial) coloring on the left is not allowed, but the (partial) coloring on the right is allowed.

There are many different proper colorings possible. Mondrian especially likes the color red, as it reminds him of father Christmas’ outfit. The first thing he wants to know is whether there exists a proper coloring in which exactly half of the 72 unit squares are colored red. Secondly, he is interested to know what the largest area is that can be colored red in a proper coloring. In such a coloring each unit square has an area of 1, each 2\times 2 square has an area of 4 and each 1\times 2 square has an area of 2. Now there are two questions the pixies have to answer:

• Question 1: Is there a proper coloring in which exactly 36 unit squares are colored red?
• Question 2: What is the largest area that can be colored red in a proper coloring?

Possible Answers

1. The correct answer to question 1 is NO; the largest red area in a proper coloring is 39.
2. The correct answer to question 1 is NO; the largest red area in a proper coloring is 40.
3. The correct answer to question 1 is NO; the largest red area in a proper coloring is 41.
4. The correct answer to question 1 is NO; the largest red area in a proper coloring is 42.
5. The correct answer to question 1 is NO; the largest red area in a proper coloring is 43.
6. The correct answer to question 1 is YES; the largest red area in a proper coloring is 39.
7. The correct answer to question 1 is YES; the largest red area in a proper coloring is 40.
8. The correct answer to question 1 is YES; the largest red area in a proper coloring is 41.
9. The correct answer to question 1 is YES; the largest red area in a proper coloring is 42.
10. The correct answer to question 1 is YES; the largest red area in a proper coloring is 43.