
© Julia Nurit Schönnagel, MATH+
Author: Svenja M. Griesbach
Project: Information Design for Bayesian Networks (AA3-9)
Challenge
To get in shape for the 24 December, Santa has been hiking in the mountains for a few days. When he arrived at the main chalet with the red door, however, he noticed that he had lost a few wish lists in one of the smaller chalets. Of course, he has to find them as quick as possible. Unfortunately, he does not remember exactly in which of the six chalets he left the wish lists; he only knows that they must be in one of them. Since Santa did not stop at all of the chalets during his hike, he can at least rule out two of the six. For each of the other four chalets, he can at least say how probable it is that the wish lists lie there.
Since Santa has no time to lose, he immediately calls Rudolph with his super-fast sleigh to help him. Just as the two are about to set off, they notice that a thick layer of snow is blocking the slopes. So first, the slopes have to be ploughed before they can be used by their sled. For this purpose, only one single magic snowplow is available, which can clear the slopes one after the other, but in completely arbitrary order. Thus, there is no extra time needed in addition to clearing the individual slopes. On his map (see Fig. 1), Santa can read off how long it takes to plough each of the slopes. Once a slope is cleared of snow, Santa and Rudolph can dash from one end of that slope to the other in their lightning-fast sleigh without wasting any time.
The two start in the main chalets with the red door. As soon as Santa finds the wish lists in one of the chalets, they stop the search as well as the clearing of the slopes.
In what order should Santa have the slopes ploughed in order to find the wish lists on average as quickly as possible?
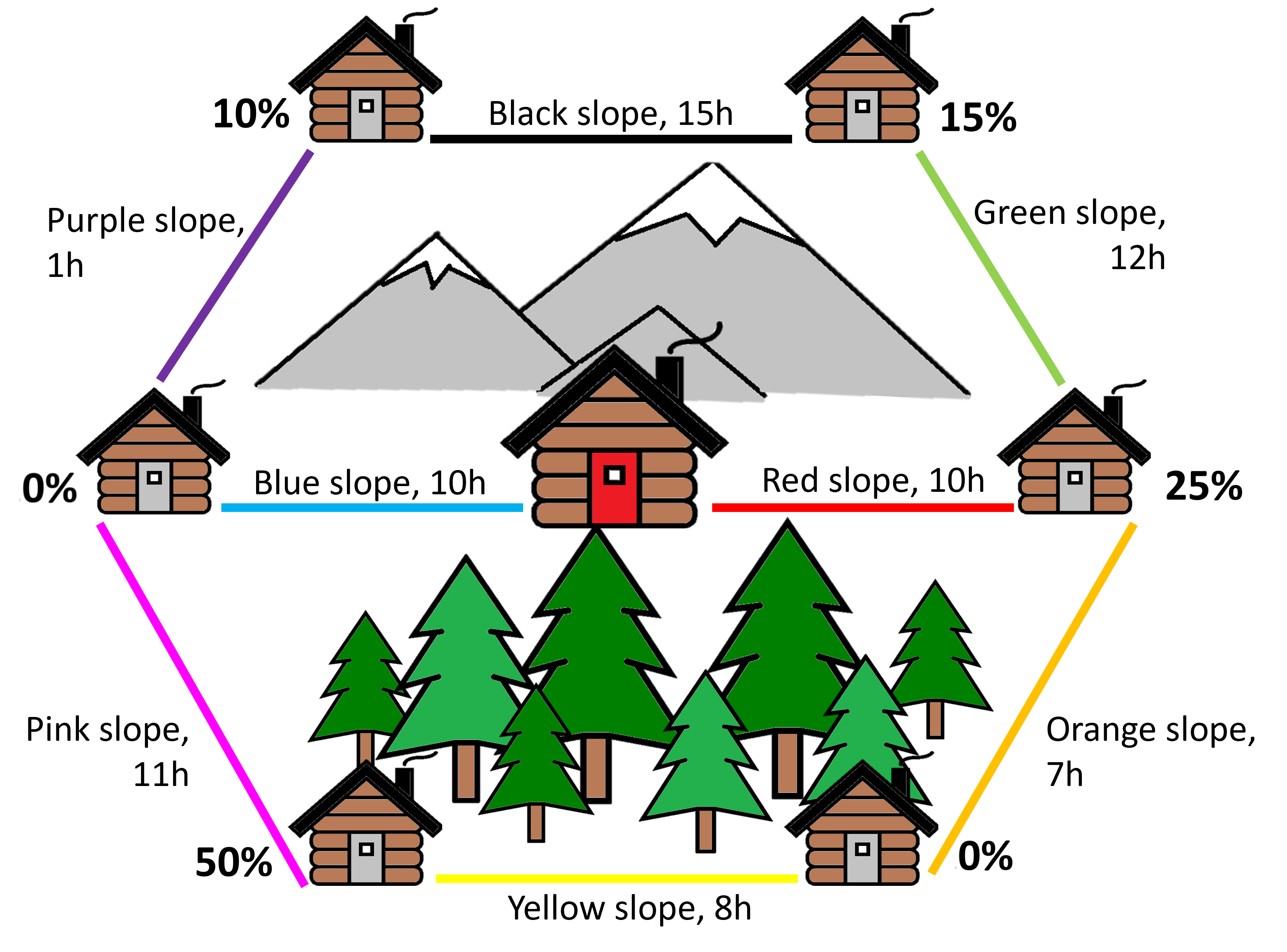
Figure 1: Santa’s map with the main chalet with the red door, the surrounding chalets (each with the probability that the wish lists lie there), and the slopes (with the respective ploughing time) between the chalets.
Possible answers:
- blue, pink, red, green, purple
- blue, pink, purple, red, green
- blue, purple, black, green, pink
- blue, purple, pink, red, green
- blue, red, purple, green, pink
- red, green, orange, yellow, blue, purple
- red, blue, purple, pink, green
- red, blue, pink, purple, green
- red, orange, yellow, green, blue, purple
- red, orange, yellow, blue, purple, black
Project reference:
The mathematical problem behind this puzzle is called expanding search, where the search can be continued at any previously reached node of a graph at any time.
In project AA 3-9 Information Design for Bayesian Networks, we consider very similar networks to Santa’s map: Bayesian networks are directed graphs consisting of weighted edges (here the slopes with their respective ploughing time) and nodes (the chalets) with a conditional probability distribution (represented by the probabilities).