MATH+ Advent Calendar
The MATH+ Advent Calendar invites you to discover the beauty and power of Math beyond the subjects covered in school.
The calendar offers fascinating insights into recent application-oriented mathematical research and into the everyday professional life of mathematicians. The 24 challenging puzzles are aimed at curious high school students, university students, teachers, and everyone interested.
You can find challenge 24 here: https://www.mathekalender.de/wp/calendar/challenges/2025-24-en/
The discussion of the solution to challenges 1 – 16 can be found here https://www.mathekalender.de/wp/forum/forum-161.html
Here you can vote for the best challenge 2025: https://www.mathekalender.de/wp/best-challenge-2025/
The registration for the calender 2025 is possible since November 1.
Here you can find the challenges from the last years:
https://www.mathekalender.de/wp/calendar/challenge-archive/.
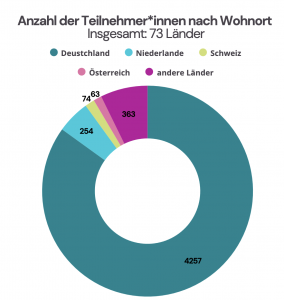
Participants 2024
In 2024, a total of 5454 participants took part in the MATH+ Advent Calendar. Our participants live in 73 countries:
More than half of the participants are pupils or teachers who take part together with their classes. However, the Advent calendar also attracts many math enthusiasts – including university students.
Particularly encouraging: Around 50% of the participants in the MATH+ Advent Calendar are girls!
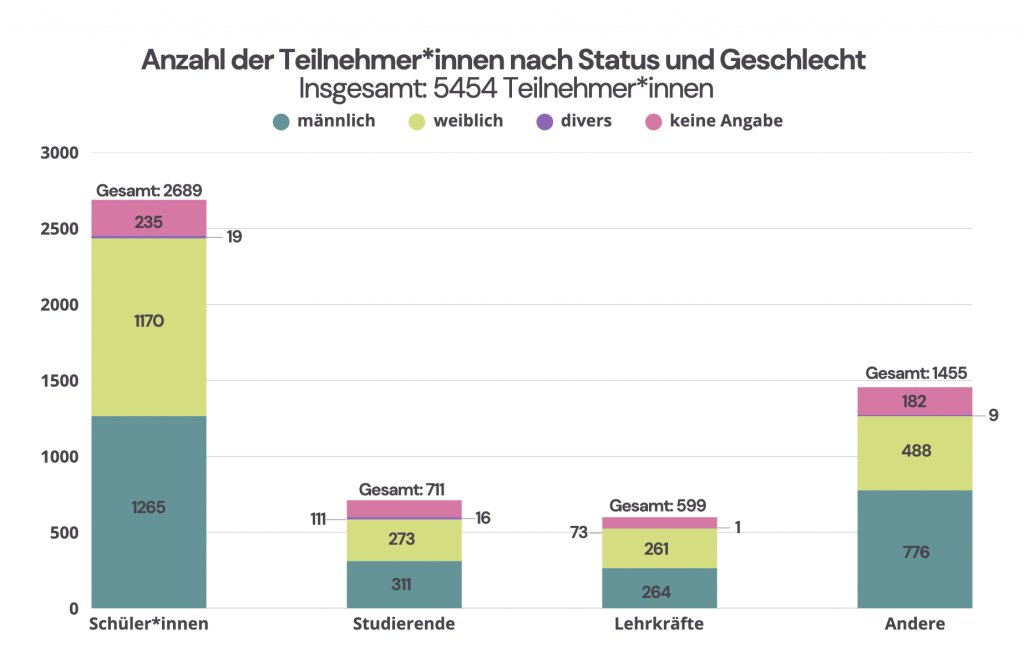
For more numbers from the recent and past MATH+ Advent Calendars, see our statistics subpage.
The Berlin Mathematics Research Center MATH+
MATH+ is a cross-institutional and interdisciplinary Cluster of Excellence based in Berlin. It sets out to explore and further develop new approaches in application-oriented mathematics. Emphasis is placed on mathematical principles for using ever larger amounts of data in life and material sciences, in energy and network research, and in the humanities and social sciences.
MATH+ is funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) for a first period of seven years since January 2019. It is a joint project of the three major universities in Berlin—Freie Universität Berlin, Humboldt-Universität zu Berlin, and Technische Universität Berlin—as well as the Weierstrass Institute for Applied Analysis and Stochastics (WIAS) and the Zuse Institute Berlin (ZIB). MATH+ continues the success stories of the renowned Research Center Matheon and the Graduate School Berlin Mathematical School (BMS).