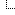I answered 2 for k = 2, too.
I used pairs of players (Pm, Pn) as graph nodes and then tried linking them together - for a good team of (P1, P2, P3), pairs (P1, P2), (P2, P3) and (P1, P3) would be connected to each other. As links are always added in threes, I was unable to keep the graph disconnected while adding links to yet unconnected pairs even with k = 2.
Yep, my graph theory knowledge is rather poor, aside of using some its parts and algorithms in coding until this challenge, and researching this section of math on the go proved to be difficult, so I admit that in this "experimental" approach I have likely overlooked some things and ended up with a wrong answer.
Ja, ich werde versuchen, die Lösung von st1974 später zu lesen und verstehen.
I used pairs of players (Pm, Pn) as graph nodes and then tried linking them together - for a good team of (P1, P2, P3), pairs (P1, P2), (P2, P3) and (P1, P3) would be connected to each other. As links are always added in threes, I was unable to keep the graph disconnected while adding links to yet unconnected pairs even with k = 2.
Yep, my graph theory knowledge is rather poor, aside of using some its parts and algorithms in coding until this challenge, and researching this section of math on the go proved to be difficult, so I admit that in this "experimental" approach I have likely overlooked some things and ended up with a wrong answer.
Ja, ich werde versuchen, die Lösung von st1974 später zu lesen und verstehen.