22 Zelda in Gefahr

© Frauke Jansen, MATH+

Autor*innen: Luise Fehlinger (HU Berlin), Florian Matthies (HU Berlin, Herder-Gymnasium Berlin)
Projekt: Arbeitsgruppe Mathematik und ihre Didaktik (HU Berlin)

Aufgabe

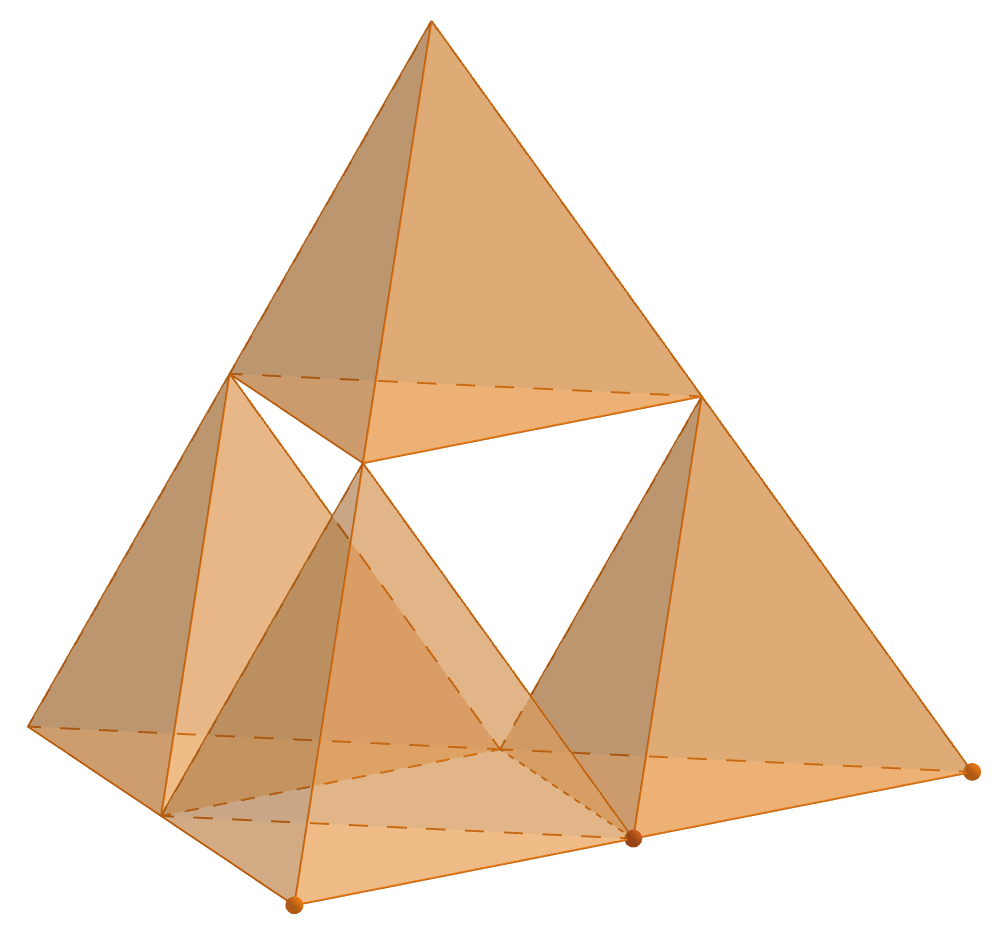
Die Prinzessin Zelda wurde schon wieder entführt. Und es ist klar, dass diesmal Mut, Kraft und Weisheit, die die Ecken des magischen Triforce bilden, nicht ausreichen werden, um sie zu retten. Es ist unbedingt auch die vierte Kraft, Geduld, nötig. Das Triforce muss also in ein magisches Tetraeder umgebaut werden. Eine neue Dimension kommt dazu. Aus dem gleichseitigen Dreieck des Triforce wird ein regelmäßiges Tetraeder. Wie beim Triforce müssen die Ecken des Tetraeders aus kleineren Tetraedern bestehen. Diese berühren sich an ihren Eckpunkten und bilden so das Gerüst des magischen Tetraeders (s. Abb. 1). Allerdings darf das Innere nicht leer bleiben. Es muss durch einen inneren Körper K_1 perfekt ausgefüllt werden, der wiederum aus Ecken und einem weiteren inneren Körper K_2 besteht usw.

Abbildung 1: Der Tetraeder K_0. Der Körper K_1 entsteht aus K_0 durch abschneiden der Ecken (in orange). K_1 ist demnach der (farblose) Rest in der Mitte des Tetraeders K_0.

Das Tetraforce ist also ein regelmäßiges Tetraeder, wir nennen diesen Körper K_0.

• K_1 entsteht aus K_0, indem man alle Ecken von K_0abschneidet. Die Schnittflächen sind dabei jeweils durch die Mittelpunkte der Kanten von K_0, die sich in dem jeweiligen Eckpunkt treffen, definiert (s. Abb. 1).
• Aus K_1 entsteht K_2 wieder durch abschneiden aller Ecken von K_1. Wieder sind die Schnittflächen durch die Mittelpunkte aller Kanten von K_1, die sich in dem jeweiligen Eckpunkt treffen, definiert.
• So geht es immer weiter: K_{n+1} entsteht aus K_n wieder durch abschneiden aller Ecken von K_n. Wieder sind die Schnittflächen durch die Mittelpunkte aller Kanten von K_n, die sich in dem jeweiligen Eckpunkt treffen, definiert.
  Nach unendlich vielen Schnitten bleibt das magische Herz des Tetraforce übrig.

 

Dieses Herz werden die Wichtel – wer sonst wäre dazu in der Lage – aus einem magischen Kristall herstellen, welches bei -40°C am magnetischen Pol der Erde aus Weihnachtselixier gegossen werden muss.

Doch welche Eigenschaften hat das magische Herz? Die Wichtel stellen verschiedene Vermutungen auf. Aber eine Aussage ist falsch. Welche?

Antwortmöglichkeiten:

1. K_1 ist ein Oktaeder.
2. Das Volumen von K_1 ist nur die Hälfte vom Volumen von K_0.
3. Alle K_n sind konvex.
4. K_0 ist der einzige der Körper, bei dem sich nur drei Kanten in jedem Eckpunkt treffen. Bei allen anderen K_n treffen sich immer vier Kanten pro Eckpunkt.
5. Jeder Körper K_n hat auch Seitenflächen, die gleichseitige Dreiecke sind.
6. Jeder Körper K_n hat als Seitenflächen nur Dreiecke und/oder Vierecke.
7. Die SeitenSchwerpunkte der Seitenflächen von K_n gehören zu allen K_{n+k} (k \in \mathbb{N}).
8. In jedem Schritt verdoppelt sich die Anzahl der Kanten.
9. Bei jedem Körper K_n außer K_0 gibt es genau zwei Seitenflächen mehr als Eckpunkte.
10. Das magische Herz ist eine Kugel.