13 Mondrian

© Frauke Jansen, MATH+

Autor: Cor Hurkens (TU Eindhoven)
Projekt: 4TU.AMI

Aufgabe

Der Malwichtel Mondrian hat eine quadratische Weihnachtskarte entworfen und diese in 121 gleichgroße quadratische Zellen unterteilt (s. Abb. 1a). In drei dieser Zellen zeichnet Mondrian einen Stern – genau so wie es in Abbildung 1a zu sehen ist.

Den Rest der Weihnachtskarte bestehend aus 118 Zellen teilt Mondrian in lauter 1×2 und 2×1 Rechtecken (bestehend aus jeweils 2 Zellen) und 2×2 Quadrate (aus jeweils 4 Zellen) ein, die er mit bunten Farben ausmalt (s. Abb. 1b). Am Ende ist jede der 118 Zellen Teil genau eines solchen Rechtecks oder Quadrats. Die drei Zellen mit den Sternen werden dabei nicht übermalt.

Abbildung 1a: Mondrians Weihnachtskarte mit den drei Sternen.

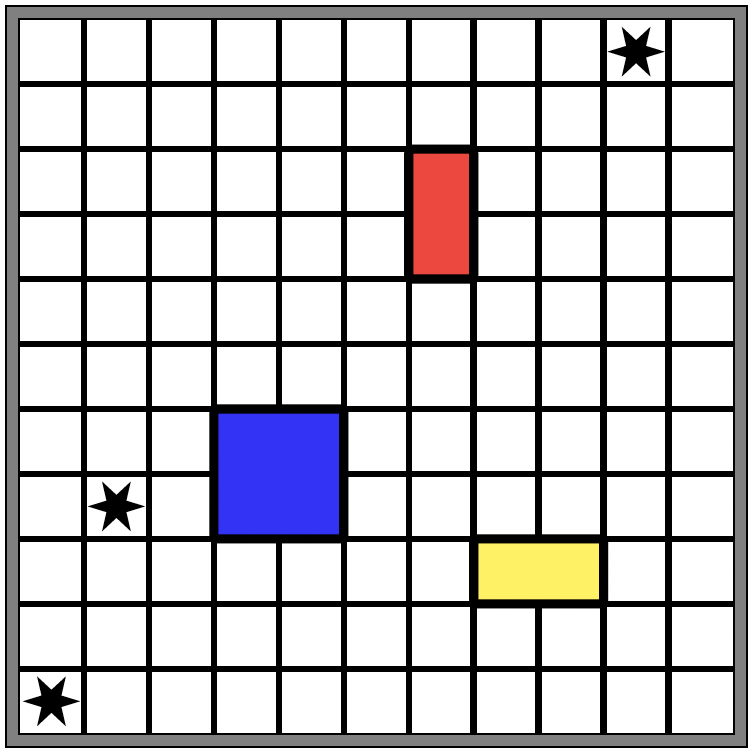
Abbildung 1b: Beispiel: Mondrians Weihnachtskarte mit zwei Rechtecken und einem Quadrat.

Wie viele 2×2 Quadrate kann Mondrian höchstens auf seine Weihnachtskarte malen?

Antwortmöglichkeiten:

1.  Die größtmögliche Zahl von 2×2 Quadraten ist 14.
2.  Die größtmögliche Zahl von 2×2 Quadraten ist 15.
3.  Die größtmögliche Zahl von 2×2 Quadraten ist 16.
4.  Die größtmögliche Zahl von 2×2 Quadraten ist 17.
5.  Die größtmögliche Zahl von 2×2 Quadraten ist 18.
6.  Die größtmögliche Zahl von 2×2 Quadraten ist 19.
7.  Die größtmögliche Zahl von 2×2 Quadraten ist 20.
8.  Die größtmögliche Zahl von 2×2 Quadraten ist 21.
9.  Die größtmögliche Zahl von 2×2 Quadraten ist 22.
10.  Die größtmögliche Zahl von 2×2 Quadraten ist 23.