11 Christbaumkugel-Mashup

© Julia Nurit Schönnagel, MATH+

Autoren: Christian Hercher (Europa-Unisversität Flensburg), Michael Schmitz (Europa-Universität Flensburg)

Aufgabe

Der Wichtel Willi bedient in diesem Jahr die Christbaumkugel-Maschine in der Weihnachtswerkstatt. Die Maschine produziert Packungen mit farbigen Christbaumkugeln. Dabei kann man die Packungsgröße und die möglichen Kugelfarben einstellen. Allerdings wählt die Maschine bei jeder Kugel, die in eine Packung kommt, eine der eingestellten Farben zufällig aus. Es kann also zum Beispiel passieren, dass nur Kugeln einer Farbe in einer Packung vorkommen, obwohl mehr als eine Farbe eingestellt war. Im Moment ist die Maschine auf 5er-Packungen mit den Farben Rot und Silber eingestellt. Nachdem Willi drei Packungen geöffnet hat, behauptet er: „Alle 5er-Packungen mit Farben Rot und Silber sind voneinander verschieden.“ Dabei bezeichnen wir zwei Packungen als gleich, wenn sie die gleiche Anzahl von Kugeln je Farbe haben, und als verschieden, wenn sie nicht gleich sind.

Wichtelin Selma erwidert: „Das kann ja gar nicht sein, da es nur sechs verschiedene Packungen dieser Art gibt.“

1. Wie viele verschiedene 10er-Packungen mit Kugeln in den Farben Rot, Silber und Grün gibt es?
2. Die Maschine ist nun auf 4er-Packungen mit den Farben Rot und Silber eingestellt. Wie groß ist die Wahrscheinlichkeit dafür, dass in einer Packung genau 3 rote Kugeln sind?
3. Die Maschine ist nach wie vor auf 4er-Packungen mit den Farben Rot und Silber eingestellt. Wie groß ist die Wahrscheinlichkeit dafür, dass zwei direkt nacheinander produzierte Packungen gleich sind?
4. Die Maschine ist nun auf 9er-Packungen mit den Farben Rot und Silber eingestellt. Wie groß ist die Wahrscheinlichkeit dafür, dass zwei direkt nacheinander produzierte Packungen gleich sind?

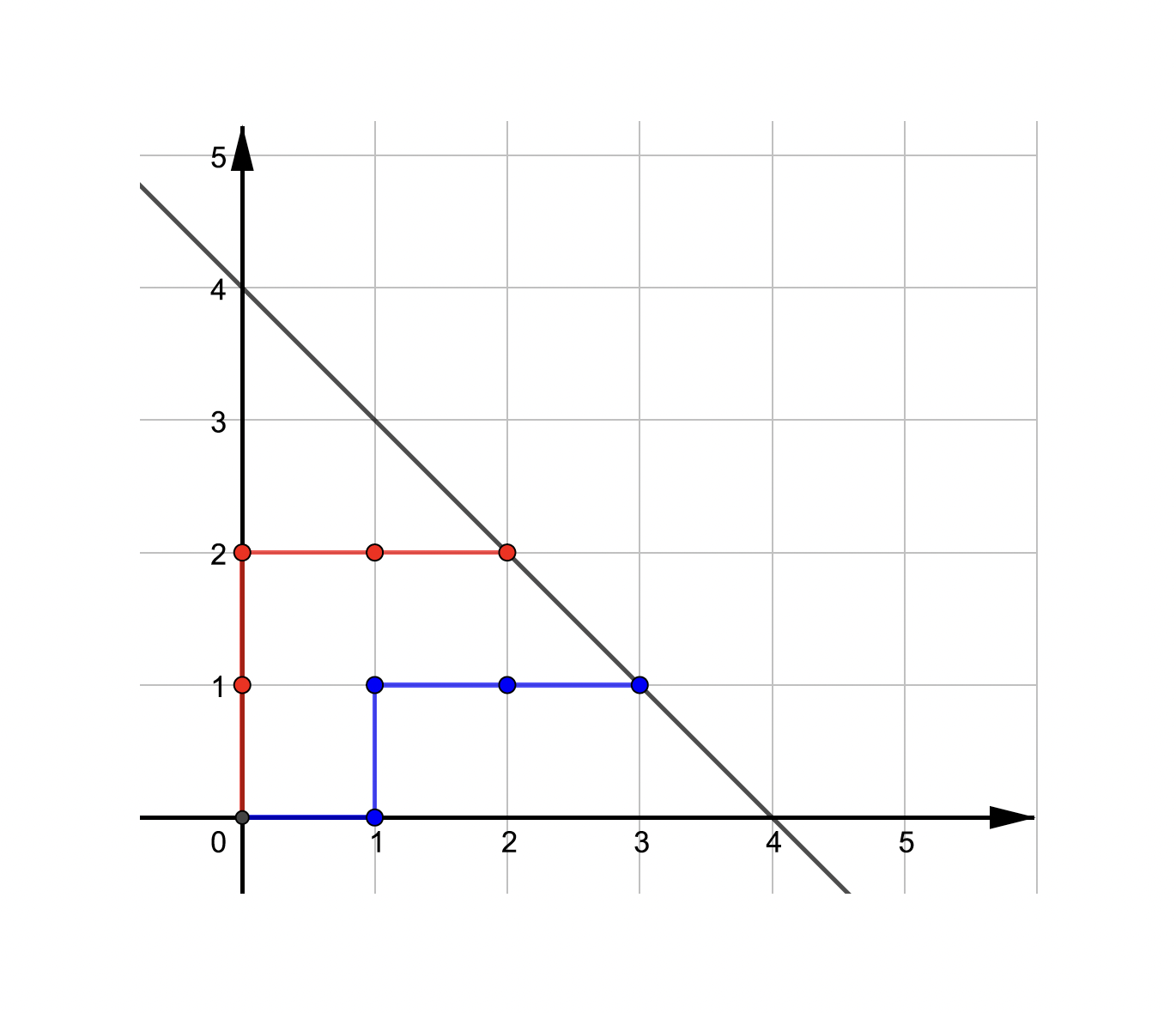
Um die Fragestellungen der Aufgabenteile (b) bis (d) zu beantworten, veranschaulicht sich die schlaue Selma den Füllvorgang bei zwei möglichen Farben, z. B. Rot und Silber, durch einen Pfad im Koordinatensystem. Kommt eine silberne Kugel in die Packung, geht es einen Schritt nach rechts, kommt eine rote Kugel in die Packung, geht es einen Schritt nach oben. In der Abbildung stellt der blaue Pfad das Befüllen einer 4er-Packung mit drei silbernen und einer roten Kugel dar. Der rote Pfad stellt das Befüllen einer 4er-Packung mit zwei silbernen und zwei roten Kugeln dar. Vielleicht hilft auch dir diese Veranschaulichung weiter?

Antwortmöglichkeiten:

1.  (a) 59049,  (c) \tfrac{35}{128}.
2.  (a) 11, (d) \tfrac{1}{10}.
3.  (b) \tfrac{1}{5}, (c) \tfrac{1}{5}.
4.  (b) \tfrac{1}{4}, (d) \tfrac{1}{10}.
5.  (c) \tfrac{35}{128}, (d) \tfrac{12055}{65536}.
6.  (a) 66, (c) \tfrac{1}{5}.
7.  (a) 59049, (d) \tfrac{12155}{65536}.
8.  (b) \tfrac{1}{4}, (c) \tfrac{35}{128}.
9.  (b) \tfrac{1}{5}, (d) \tfrac{12155}{65536}.
10.  (c) \tfrac{1}{5}, (d) \tfrac{12055}{65536}.