
© Friederike Hofmann, MATH+
Autor: Silas Rathke (FU Berlin)
Aufgabe
In der Bar „Zum Tropfenden Eiszapfen” geht der Nikolaus seiner Lieblingsbeschäftigung nach: Er redet unentwegt über sein Haus. Was für eine architektonische Meisterleistung es doch sei! In seiner Schlichtheit elegant verbinde es prägende Elemente der Neoromanik mit der Scheldegotik! Und trotz dieser intellektuellen Glanzleistung weiß noch immer jedes Kind, wie es aussieht! Voller Stolz präsentiert er schließlich seiner gelangweilten Zuhörerschaft eine Zeichnung seines so verehrten Hauses (siehe Abb. 1).
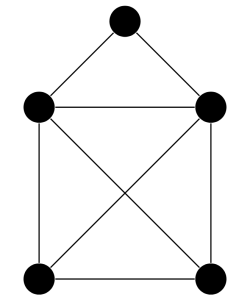
Abbildung 1: Das Haus vom Nikolaus bestehend aus fünf Kreisen und acht Verbindungslinien.
„Und das Beste kommt erst noch!”, lässt er sein unfreiwilliges Publikum wissen. „Wenn man erst einmal die fünf schwarzen Kreise gemalt hat, kann man alle acht Linien zwischen den Kreisen zeichnen, ohne den Stift abzusetzen und ohne eine Linie doppelt zu malen!”
Jetzt wird es dem anwesenden Mathematiker-Elf Uhur zu bunt und er antwortet mit einem seiner Lieblingssätze: „Beweise es!”
Der Nikolaus erstarrt. Immerhin hat er in seinem Redeschwall den einen oder anderen Glühwein getrunken und so fällt ihm nun beim besten Willen nicht mehr ein, wie man sein Haus mit der oben genannten Regel zeichnen kann. Es bleibt ihm nichts anderes übrig, als zufällig zu zeichnen und das Beste zu hoffen.
Er holt einen dicken roten Filzstift aus seinem Sack und beschließt die dünnen schwarzen Linien in der Zeichnung des Hauses vom Nikolaus mit dem Filzstift nachzuzeichnen.
Dafür wählt er uniform zufällig (uniform zufällig bedeutet in diesem Fall, dass alle Kreise mit der gleichen Wahrscheinlichkeit gewählt werden) einen der fünf Kreise als Startpunkt und setzt dort seinen Stift an. Von da an zeichnet er die nächste Linie immer auf die folgende Art: Er schaut sich an, wo sein Stift gerade ist, schaut welche Linien bei der schwarzen Zeichnung diesen Kreis als Endpunkt haben und noch nicht nachgezeichnet sind. Von diesen wählt er uniform zufällig und unabhängig von seinen vorherigen Entscheidungen eine aus und zeichnet sie mit dem Filzstift nach. Das macht er so lange, bis sein Stift einen Punkt erreicht, wo schon alle Linien rot nachgezeichnet sind.
Es sei p die Wahrscheinlichkeit, dass er dann tatsächlich das vollständige Haus des Nikolaus nachgezeichnet hat. Was ist die 100. Stelle nach dem Komma in der Dezimaldarstellung von p?
Antwortmöglichkeiten
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 0