
© Till Hausdorf, MATH+
Autor*innen: Hajo Broersma, Pim van ’t Hof (Universiteit Twente)
Projekt: 4TU.AMI
Aufgabe
Es ist ein offenes Geheimnis, dass alle Elfen, die für den Weihnachtsmann arbeiten, gerne Bogenschießen, Mathematik aber nicht leiden können. Um ihre Begeisterung für Mathematik zu steigern, hat der Weihnachtsmann die drei Elfen Archy, Bowy und Curvy zu einer Kombination aus Bogenschießen und Mathematik eingeladen.
Der Weihnachtsmann hat dafür eine runde Zielscheibe aufgestellt. Die Elfen bekommen jeweils fünf Pfeile und müssen diese nacheinander mit ihrem Bogen auf die Zielscheibe schießen. Die Zielscheibe besteht aus einem kreisförmigen Zentrum und drei konzentrischen, um das Zentrum herum angeordneten Ringen, wie in Abbildung 1 dargestellt.
Abbildung 1: Die kreisförmige Zielscheibe.
Dem Zentrum und jedem der Ringe ist jeweils eine feste Punktzahl für jeden Pfeil zugeordnet, der das entsprechende Zielgebiet trifft. Die Elfen wissen, dass diese Punktzahl aus der unendlichen Menge von Werten
\{5, 10, 15, 20, 25, 30, \ldots\}
ausgewählt wurden. Jede Punktzahl ist also ein positives Vielfaches von 5 und kann beliebig groß sein. Die genauen Punktzahlen sind nur dem Weihnachtsmann bekannt, nicht aber den Elfen. Die Elfen wissen jedoch Folgendes: Beginnend mit dem äußersten Ring steigt die Punktzahl strikt an, sodass schließlich das Zentrum die höchste Punktzahl aller vier Zielbereiche hat
Nachdem ein Elf alle fünf Pfeile auf die Zielscheibe geschossen hat, gibt der Weihnachtsmann die Gesamtpunktzahl bekannt, ohne die Punktzahlen, die die einzelnen Pfeile erzielt haben, zu nennen. Der Weihnachtsmann fordert die Elfen auf, durch geschicktes Schießen auf die Scheibe, so viele Informationen wie möglich über die Punktzahl des Zentrums zu erhalten. Wenn es einem der Elfen zum Beispiel gelänge, alle fünf Pfeile in das Zentrum zu schießen, könnten die Elfen aus der vom Weihnachtsmann verkündeten Gesamtpunktzahl sofort den genauen Wert des Zentrums erschließen. Leider sind die Elfen nicht so treffsicher, obwohl es allen dreien gelingt, das Zentrum mindestens einmal zu treffen.
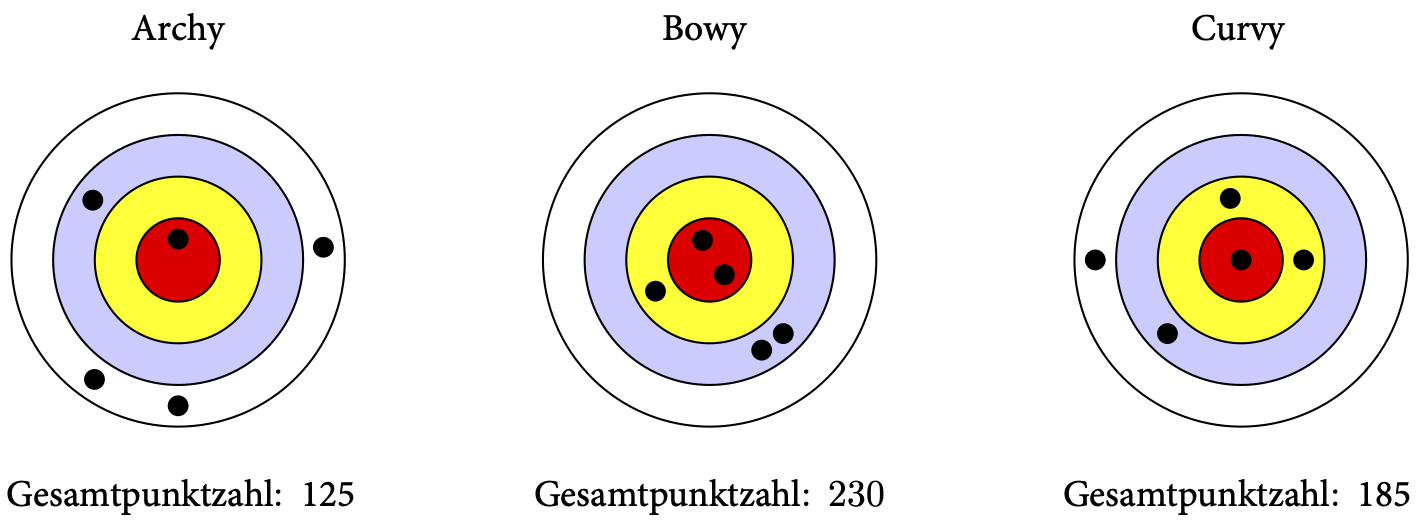
Abbildung 2: Die Punkte, an denen die Pfeile von Archy, Bowy und Curvy das Ziel getroffen haben sowie die entsprechenden Gesamtpunktzahlen der drei Elfen.
Die schwarzen Punkte in Abbildung 2 zeigen die Stellen an, an denen die Pfeile der drei Elfen die Zielscheibe getroffen haben. Die erste Zielscheibe zeigt an, dass Archy den äußeren Ring mit drei Pfeilen, den nächsten Ring mit einem Pfeil und das Zentrum mit einem Pfeil getroffen hat. Der Weihnachtsmann verrät, dass Archys Gesamtpunktzahl 125 beträgt. Aus der zweiten Zielscheibe geht hervor, dass Bowy mit einer Gesamtpunktzahl von 230 der bessere Bogenschütze ist. Schließlich, nachdem auch Curvys fünf Pfeile das Ziel getroffen haben, wie auf der dritten Zielscheibe dargestellt, verrät der Weihnachtsmann eine Gesamtpunktzahl von 185 für Curvy.
Mit diesen drei Gesamtergebnissen ist es den Elfen leider nicht möglich, den genauen Wert des Zentrums zu bestimmen. Die obigen Angaben schränken jedoch die Anzahl der möglichen Punktzahlen erheblich ein.
Welche der folgenden Aussagen ist richtig?
Antwortmöglichkeiten:
- Die Anzahl der möglichen Punktwerte für das Zentrum reduziert sich auf genau 2.
- Die Anzahl der möglichen Punktwerte für das Zentrum reduziert sich auf genau 3.
- Die Anzahl der möglichen Punktwerte für das Zentrum reduziert sich auf genau 4.
- Die Anzahl der möglichen Punktwerte für das Zentrum reduziert sich auf genau 5.
- Die Anzahl der möglichen Punktwerte für das Zentrum reduziert sich auf genau 6.
- Die Anzahl der möglichen Punktwerte für das Zentrum reduziert sich auf genau 7.
- Die Anzahl der möglichen Punktwerte für das Zentrum reduziert sich auf genau 8.
- Die Anzahl der möglichen Punktwerte für das Zentrum reduziert sich auf genau 9.
- Die Anzahl der möglichen Punktwerte für das Zentrum reduziert sich auf genau 10.
- Die Anzahl der möglichen Punktwerte für das Zentrum reduziert sich auf genau 11.
Serverprobleme: Für diese Aufgabe gibt es eine Zeitgutschrift von 72 Stunden.