11 Wunderschönes Geschenkpapier mit einem Spirographen gestalten

© Zyanya Santuario

Autorin: Eva Deinum (Wageningen University & Research)
Projekt:  4TU.AMI

Aufgabe

Die Elfen benutzen einen Spirographen, um Geschenkpapier für Weihnachten zu verzieren.
Dieser Spirograph besteht aus einem beweglichen inneren Zahnrad mit n Zähnen und einem festen äußeren Ring mit N Zähnen, wobei N>n gilt. Das innere Zahnrad sowie der äußere Ring sind kreisförmig. Die Zähne des inneren Zahnrads und des äußeren Rings passen exakt ineinander, sodass das innere Zahnrad nicht zwischen den Zähnen des äußeren Rings rutschen kann, sondern sich nur entlang des Rings abrollen lässt. Das innere Zahnrad besitzt ein vom Mittelpunkt versetztes Loch für einen Stift. In Abbildung 1 ist links der Spirographaufbau dargestellt; das Loch für den Stift ist durch einen blauen Punkt markiert.

Wenn das innere Zahnrad entlang des äußeren Rings abgerollt wird und der Stift durch das Loch gleichzeitig auf das Papier gedrückt wird, lassen sich geschlossene Kurven wie die violette Kurve auf der linken Seite von Abbildung 1 zeichnen. Eine solche geschlossene Kurve entsteht, wenn das innere Zahnrad so lange am äußeren Ring abgerollt wird, bis es wieder zu seiner ursprünglichen Position zurückkehrt (einschließlich der Lage des Lochs für den Stift). Die so erzeugten Kurven können unterschiedliche Symmetrien besitzen und sich auch selbst schneiden.
So schneidet sich beispielsweise die violette Kurve in Abbildung 1 selbst und besitzt eine 7-fache (Rotations-)Symmetrie. Eine n-fache Rotations-Symmetrie bedeutet dabei, dass eine Drehung um den Mittelpunkt des äußeren Rings um den Winkel \frac{360^\circ}{n} die Kurve auf sich selbst abbildet; nach n Anwendungen der zur Symmetrie gehörenden Rotation ergibt sich dann eine vollständige 360^\circ-Drehung.

Durch die Wahl unterschiedlicher Werte von n und N können die Elfen viele verschiedene Kurven erzeugen.
Auf der rechten Seite von Abbildung 1 sind zwei weitere Beispiele dargestellt: Die obere Kurve besitzt 7-fache Symmetrie und schneidet sich selbst; die untere besitzt 8-fache Symmetrie und schneidet sich nicht selbst.

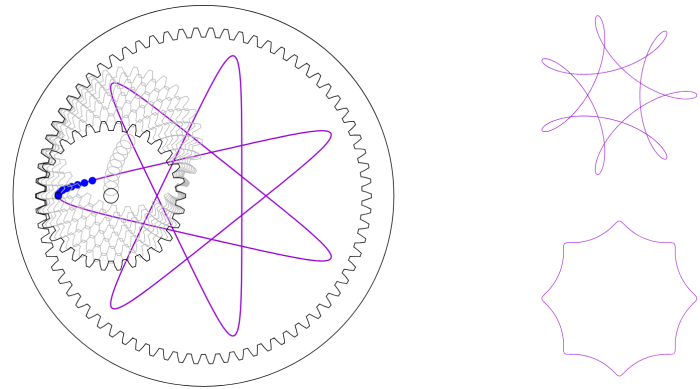
Abbildung 1: Spirographaufbau (links) mit der eingezeichneten violetten Kurve; Beispiele für Kurven mit anderen Werten von n und N (rechts).

Heute ist ein junger Elf dafür verantwortlich, das Geschenkpapier zu gestalten. Leider versteht er den Spirographen noch nicht vollständig, und es ist niemand da, der ihm helfen könnte. Er möchte eine Kurve zeichnen, die die folgenden Eigenschaften besitzt:

1. Die Kurve hat 5-fache Symmetrie.
2. Die Kurve schneidet sich selbst.

Dem jungen Elf stehen drei äußere Ringe zur Verfügung: N=100, N=115 und N=144. Außerdem gibt es sechs innere Zahnräder: n=20, n=23, n=36, n=40, n=46 und n=69. Wie viele verschiedene Kombinationen aus äußerem Ring und innerem Zahnrad kann der Elf wählen, um eine Kurve zu erzeugen, die beide gewünschten Eigenschaften erfüllt?

Antwortmöglichkeiten

1. 1 Kombination
2. 2 Kombinationen
3. 3 Kombinationen
4. 4 Kombinationen
5. 5 Kombinationen
6. 6 Kombinationen
7. 7 Kombinationen
8. 8 Kombinationen
9. 9 Kombinationen
10. Ohne zu wissen, wo sich das Loch im inneren Zahnrad befindet, kann man die Anzahl der gesuchten Kombinationen nicht eindeutig bestimmen.