
© Ivana Martić, MATH+
Ein interaktives Tool zur Aufgabe gibt es hier.
Autor: Lukas Protz (MATH+)
Aufgabe
Der eifrige Elf Eifi hat viele Drohnen gekauft, um bei der Arbeit am Nordpol zu helfen. Leider sind die Elfen in der IT-Abteilung nicht so eifrig wie Eifi und sagen ihm, dass sie derzeit keine Kapazitäten haben, um die Drohnen zu programmieren. Deshalb möchte Eifi die Drohnen selbst programmieren. Aber nicht, um bei der tatsächlichen Arbeit zu helfen, nein, er möchte mit den Drohnen eine Lichtershow veranstalten, um seine Mitelfen zu unterhalten und ihnen helfen, sich zu entspannen und den Weihnachtsstress für eine Weile zu vergessen.
Eifi hat sich bereits einige Flugrouten für die Drohnen überlegt. Er führt ein Koordinatensystem ein, dessen Mittelpunkt sich genau am Nordpol befindet. Der Einfachheit halber nimmt er an, dass die Fläche um den Nordpol herum perfekt eben ist. Die Einheiten des Koordinatensystems sind Elfen-Meilen, die Standard-Entfernungseinheit am Nordpol. Die Flugrouten, die Eifi im Sinn hat, hängen von zwei positiven ganzen Zahlen a, b ab und können in Abhängigkeit von der Zeit wie folgt parametrisiert werden:
\gamma(t) = (\sin(at),\sin(bt)),\quad 0\le t< 2\pi.
Anmerkung: Für jeden Wert t gibt die Formel die beiden Koordinaten der Flugroute zum Zeitpunkt t an. Selbstverständlich wird die Zeit t in der Standard-Zeiteinheit am Nordpol gemessen, der Elfen-Minute. Ferner ist \sin(t) eine Funktion bezüglich des Bogen- und nicht bezüglich des Gradmaßes, d.h. \sin(\pi)=0, aber \sin(180) \approx -0.8011 \neq 0.
Eifrig wie Eifi ist, probiert er einige Kombinationen von a, b aus und lässt die Drohnen eine nach der anderen fliegen, aber … oh nein. Bei einer der Kombinationen beginnen die Drohnen ab einem bestimmten Punkt der Route ihre Flugrichtung umzukehren und genau den Weg zurückzufliegen, den sie gekommen sind, wodurch sie mit anderen Drohnen zusammenstoßen. Eifi bricht das Experiment sofort ab. Er fragt sich: Für welche Kombinationen von a, b kann das passieren? Kannst du Eifi dabei helfen, alle Paare von a, b zu finden, für die die Drohnen ab einem bestimmten Punkt beginnen, den Weg zurückzufliegen, den sie gekommen sind, damit er seine Versuche, die schönste Flugroute zu finden, ohne weitere Unfälle fortsetzen kann?
Bemerkung: Für jede reelle Zahl \alpha ist \sin(\alpha) definiert als die vertikale Koordinate des Punktes auf dem Einheitskreis, den man erhält, wenn man ausgehend von dem Schnittpunkt des Einheitskreises mit der rechten Seite der horizontalen Achse entgegen dem Uhrzeigersinn den Winkel \alpha im Bogenmaß misst. Der Einheitskreis ist definiert als der Kreis mit Radius 1, dessen Mittelpunkt der Koordinatenursprung ist.
Abbildung 1 veranschaulicht diese Definition und in Abbildung 2 ist der Graph der Sinus-Funktion für \alpha zwischen -\pi und 3\pi dargestellt.
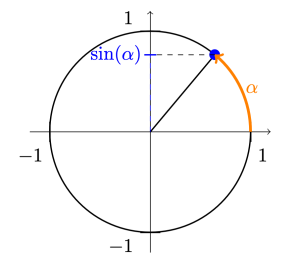
Abbildung 1: Veranschaulichung der Definition von \sin(\alpha).
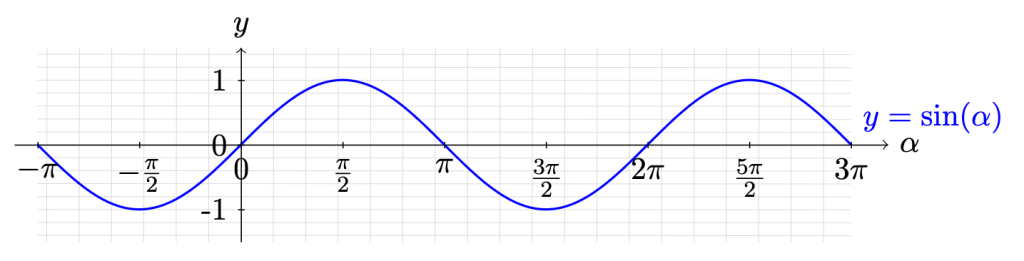
Abbildung 2: Der Graph der Sinus-Funktion.
Antwortmöglichkeiten
- Bei keiner Kombination von a und b passiert dies. Eifi hat die Drohnen einfach falsch programmiert.
- Es gibt genau eine Kombination von a und b, bei der dies passiert. Eifi hatte einfach das Pech, die Drohnen mit genau dieser Kombination getestet zu haben.
- Es gibt nur endlich viele Kombinationen von a und b, für welche dies passiert.
- Dies kann nur passieren, wenn a=b.
- Dies kann nur passieren, wenn a und b teilerfremd sind, d.h. keine gemeinsamen positiven Teiler außer der 1 haben.
- Dies kann nur passieren, wenn a und b nicht teilerfremd sind, d.h. einen gemeinsamen Teiler größer als 1 haben.
- Dies passiert genau dann, wenn a und b beide Zweierpotenzen sind oder wenn a=b gilt.
- Dies passiert genau dann, wenn die höchste Zweierpotenz die a teilt auch die höchste Zweierpotenz ist, die b teilt.
- Dies passiert für alle Kombinationen von a und b, wenn beide Zahlen gößer als 2025^{2025} sind.
- Keine der anderen Antworten ist richtig.