23 Herr Johnsons zerbrochene Weihnachtsanhänger

© Julia Nurit Schönnagel, MATH+

Autoren: Zoe Geiselmann und Kevin Kühn
Projekt: EF-LI-Opt-1

Aufgabe

Herr Johnson liebt Weihnachten und hat fünf selbst gebaute Weihnachtsbaumanhänger, die ihm besonders viel bedeuten. Leider hat seine Katze Rhombi im vergangenen Jahr zwei davon zerbrochen. Um rechtzeitig zu Heiligabend wieder alle seine Lieblingsanhänger am Weihnachtsbaum zu haben, möchte Herr Johnson die beiden beschädigten Anhänger neu anfertigen.
Zum Glück weiß er noch, wo er die benötigten Netze kaufen kann. Dabei handelt es sich um flache Vorlagen der Anhänger, die an den richtigen Stellen gefaltet und zusammengeklebt werden müssen, um dreidimensionale Körper zu erhalten.

Er kauft das gleiche Paket mit fünf Netzen, das er bereits vor einigen Jahren gekauft hat und aus dem sich die fünf verschiedenen Anhänger herstellen lassen, die ihm so viel Freude bereitet haben. Allerdings besitzt er noch drei unbeschädigte Anhänger, die immer noch wie neu aussehen!
In Abbildung 1 sind die noch vorhandenen intakten Anhänger von Herrn Johnson zu sehen, in Abbildung 2 die fünf neu gekauften Netze (A–E).

Hilf Herrn Johnson dabei, den Überblick zu behalten. Bestimme die beiden Netze, aus denen Weihnachtsanhänger entstehen, die nicht zu den bereits vorhandenen Anhängern in Abbildung 1 gehören.

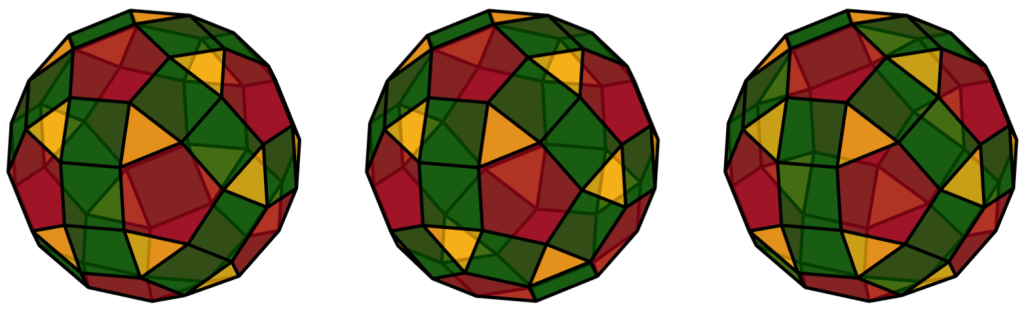
Abbildung 1: Die drei noch intakten Weihnachtsanhänger.

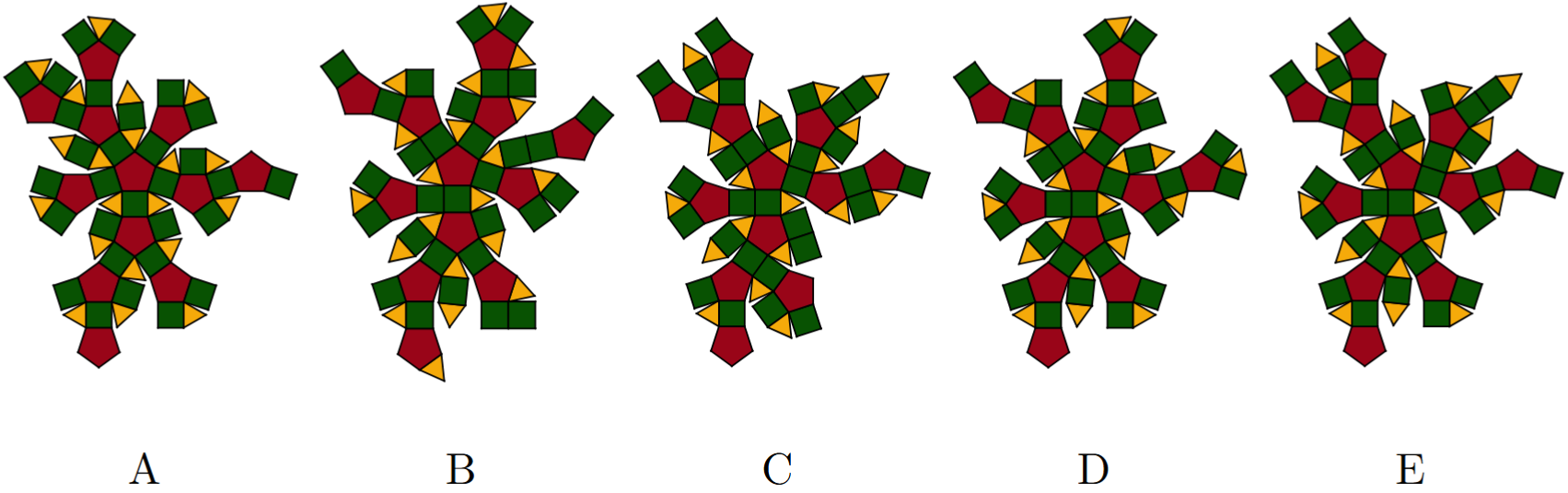
Abbildung 2: Die fünf Netze (A–E), aus denen Weihnachtsanhänger gefaltet werden können.

Antwortmöglichkeiten:

1. A und B
2. B und E
3. A und C
4. C und D
5. B und D
6. A und E
7. A und D
8. B und C
9. D und E
10. C und E

Projektbezug:

Im Projekt EF-LI-Opt-1 werden algebraisch-geometrische Objekte mit kombinatorischen und diskreten Methoden untersucht. Polytope treten auf natürliche Weise an der Schnittstelle dieser Disziplinen auf, von denen drei in der Aufgabe dargestellt sind.