3 Farbenfrohe Weihnachten

© Ivana Martić, MATH+

Autor: Hajo Broersma

Projekt: 4TU.AMI

Aufgabe

Der Maler-Elf Mondrian hat eine rechteckige Weihnachtskarte entworfen, wie in Abbildung 1 dargestellt wird. Die Fläche  der Größe 8 \times 12 ist in folgende Bereiche unterteilt: 72 Einheitsquadrate (1 \times 1), drei 2 \times 2 Quadrate und sechs 1 \times 2 Rechtecke.

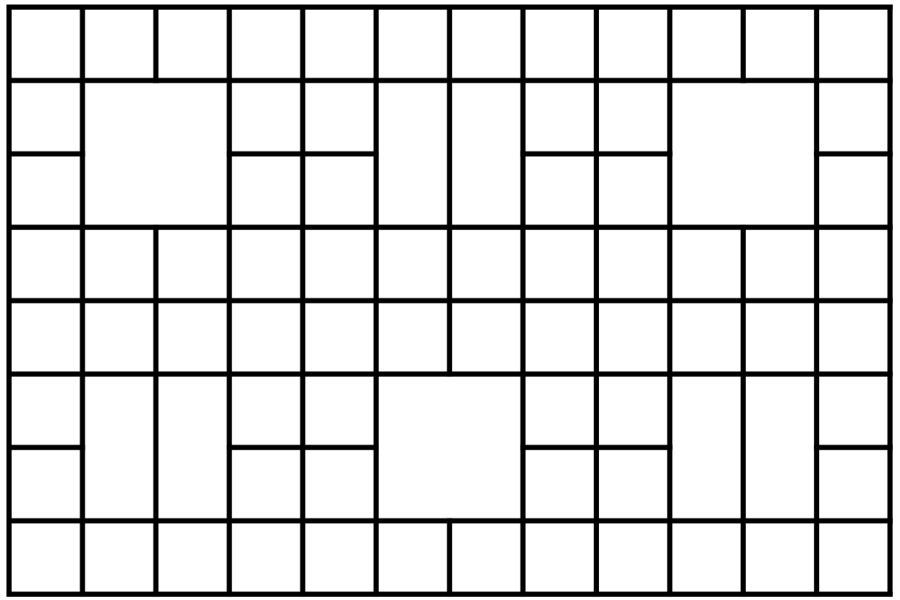
Abbildung 1: Die unbemalte Weihnachtskarte.

Mondrian bittet drei Feen, die verschiedenen Bereiche der Karte mit Rot, Gelb und Blau zu bemalen. Jeder Bereich – egal ob (1 \times 1) Einheitsquadrat, 2 \times 2 Quadrat oder 1 \times 2 Rechteck – soll mit genau einer der drei Farben eingefärbt werden.

Die fertige Färbung ist nur dann zulässig, wenn an keiner Stelle zwei Felder der gleichen Farbe eine gemeinsame Kante besitzen, während sie sich aber an einer Ecke berühren dürfen. Abbildung 2 verdeutlicht diese Regel an zwei Beispielen.

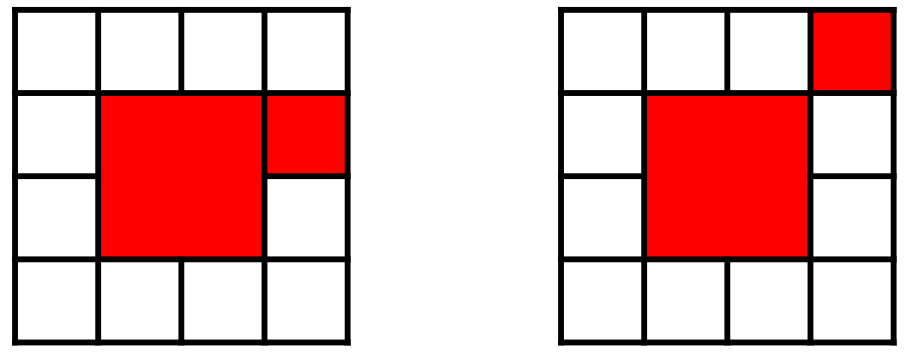
Abbildung 2: Die (ausschnittsweise) Färbung auf der linken Seite ist nicht zulässig, die auf der rechten Seite ist zulässig.

Es sind viele unterschiedliche zulässige Färbungen möglich. Mondrian hat eine besondere Vorliebe für die Farbe Rot, da sie ihn an den Anzug des Weihnachtsmanns erinnert. Daher möchte er zunächst wissen, ob eine zulässige Färbung existiert, bei der genau die Hälfte der 72 Einheitsquadrate rot bemalt wird.

Außerdem interessiert ihn, was die größtmögliche Fläche ist, die man bei einer zulässigen Färbung rot bemalen kann. Dabei hat jedes Einheitsquadrat die Fläche 1, jedes 2 \times 2 Quadrat die Fläche 4 und jedes 1 \times 2 Rechteck die Fläche 2.

Die Feen müssen nun also die folgenden beiden Fragen beantworten:

• Frage 1: Gibt es eine zulässige Färbung, bei
  der genau 36 Einheitsquadrate rot bemalt werden?
• Frage 2: Was ist die größtmögliche Fläche, die bei einer zulässigen Färbung rot bemalt werden kann?

Antwortmöglichkeiten

1. Die korrekte Antwort auf Frage 1 ist NEIN; die größtmögliche rote Fläche in einer zulässigen Färbung ist 39.
2. Die korrekte Antwort auf Frage 1 ist NEIN; die größtmögliche rote Fläche in einer zulässigen Färbung ist 40.
3. Die korrekte Antwort auf Frage 1 ist NEIN; die größtmögliche rote Fläche in einer zulässigen Färbung ist 41.
4. Die korrekte Antwort auf Frage 1 ist NEIN; die größtmögliche rote Fläche in einer zulässigen Färbung ist 42.
5. Die korrekte Antwort auf Frage 1 ist NEIN; die größtmögliche rote Fläche in einer zulässigen Färbung ist 43.
6. Die korrekte Antwort auf Frage 1 ist JA; die größtmögliche rote Fläche in einer zulässigen Färbung ist 39.
7. Die korrekte Antwort auf Frage 1 ist JA; die größtmögliche rote Fläche in einer zulässigen Färbung ist 40.
8. Die korrekte Antwort auf Frage 1 ist JA; die größtmögliche rote Fläche in einer zulässigen Färbung ist 41.
9. Die korrekte Antwort auf Frage 1 ist JA; die größtmögliche rote Fläche in einer zulässigen Färbung ist 42.
10. Die korrekte Antwort auf Frage 1 ist JA; die größtmögliche rote Fläche in einer zulässigen Färbung ist 43.